Heat exchange for an isolated container

[Kalkunipraed]

Short version:

If I have an insulated container(box) of some specific size. The inside temperature is temperature X. Ambient temperature is Y. Also X < Y. The box starts warming up. I log the inside temperature over time with data points.
How can I determine one or more of the following based on the data points:

A) The amount of energy gained in Watts (for some specific temperature difference)
B) Thermal resistance value for the box
C) Thermal conduction value for the box

Long version:

I am a homebrewer and built an insulated box for fermentation.

The container has walls of 5cm polystyrene (EPS), 2cm polystyrene(XPS) and 6mm plywood.

The container outer dimensions are height: 72cm(23.3inches), width and length 60cm(23.6 inches).
Inner height: 56cm(22 inches), width and depth 45cm(17.7 inches)

I took it outside where it was about 7C(44.6F) and left it there to cool it down. Then put the lid on and the temperature controller thermometer in and brought it inside where the ambient temperature was 22-23C (71.7-73.4F). I took notes how the temperature changed over time inside the box. Time units are in minutes. I didn't wait until it got to ambient, but it got rather close.

Sample data points:
0 - 7.9 C
30 - 10 C
59 - 12.9 C
100 - 16.0 C

or

0 - 46.2 F
30 - 50 F
59 - 55.2 F
100 - 60.8 F

The graph with full collected data and Celsius values:

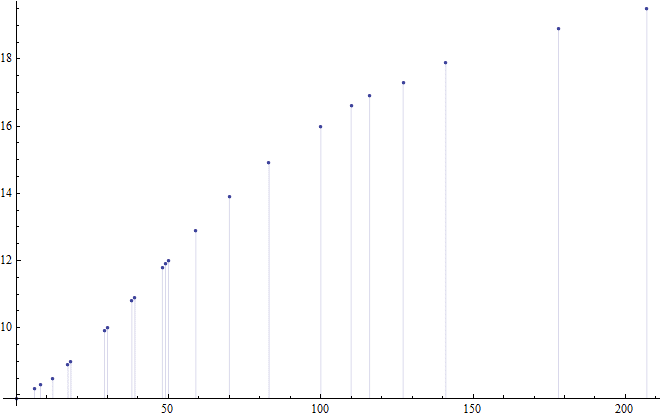
How can I determine the amount of Watts seeping into my box for any temperature difference? The answer I am trying to get is something like: for a temperature difference of 7C, the box receives 12W/h. Or anything that gives me more-or-less accurate wattage in any form.

This would help me determine how much cooling I need for the container.

I looked around the web for several hours without finding a solution. Or some solutions that I tried suggested only ~1-2W/h, which is way too low. My very rough calculations based on the insulation type suggest it should be at east 11-12W/h. I do not have the incorrect equations at hand because I am at work.

So I would be very glad if someone could help me with this.

Thank you in advance!

 

[Kalkunipraed]

For example, I found a calculation showing how much energy is needed to heat a cubic meter of air by 1C.

The weight of air is 1.205 kg/m3 @ 20C
The specific heat capacity of air is 1.005 kj/kg @ 20C

So If my inner area is 0.1134 m^3, then to raise the temperature of it by 5C i would require:
1.205 * 1.005 * 5 * 0.11 = 0.66 kJ = 0.19W/h

I know that my boxes inside temperature rose 5 degrees in an hour, so it would seem that with my 60W of pure cooling power, the coolers would have to work for about 12 seconds in an hour. This doesn't seem right. What am I missing?

Another thread on this forum gave an example of a 100W light bulb working in 1m3 space:
The specific heat of air is 716 J/kG K. The density of air is 1.3 kg/m^3. 1 watt is 1 J/sec.
So. In 60 seconds, you'd get a temperature rise of:
100*60/716/1.3=6.5 C

According to this:
0.19*3600/716/(1.3*0.11) = 6.7C/hour @ 0.19 W/h
and
0.142*3600/716/(1.3*0.11) = circa 5C/hour @ 0.142W/h

This just seems like a ridiculously small amount of energy.

And a third one. This includes an estimation on the insulation value, which I would like to avoid:

0.03 Rough(+-0.01) Watts/Meter/Kelvin value for my insulation
1.925 Outside area of the box (m^2)
15 Example temperature difference in C
0.076 Average thickness of insulation in meters

(0.03)*(1.925)*(15)/(0.076) = 11.4 Watts of leakage

Which one of those(if any) is on the right track?
Am I totally missing something?

Thanks

 

[Chestermiller]

The basic equation is going to be:
WC_p\frac{dT}{dt}= \frac{(T_0-T)}{R}=Q
where T is the temperature of the gas in the box, T₀ is the outside temperature, t is time, W is the mass of gas in the box, C_p is the heat capacity of the gas, and R is the lumped resistance to heat transfer through the walls of the box and to the outside.

In order to do what you want to do, you need to determine R. There are two ways of doing this:

1. Use the geometry of the walls and the thermal conductivities of the walls to calculate R. The calculation must also include the convective heat transfer resistance between the outside wall of the box and the surrounding air.

2. Use your experimental data to determine the value of R.

Once you know R, you can determine the heat loss rate Q.

Since you have actual experimental data on the heating, the preferred method is method 2.

The solution to the heat transfer equation for the temperature inside the box is:

\frac{(T_0-T)}{(T_0-T_{initial})}=e^{-\frac{t}{WC_pR}}
or equivalently
\ln{(T_0-T)}=\ln{(T_0-T_{init})}-\frac{t}{WC_pR}
So you make a plot of $\ln{(T_0-T)}$ versus t, and the slope is $\frac{1}{WC_pR}$. The easiest way to do this is to use a semi-log plot.

Chet

 

[Kalkunipraed]

If I understood your initial equation correctly, it means to core of the calculation is:
WC_p\frac{dT}{dt}

For example to raise 5C in 1hour:
0.14 * 1005\frac{5}{3600}=0.195...W/h
And Joules needed to heat that amount of air by 5C
0.14*1005*5=702Joules

All this seems to be the second equation indicated on this page: http://www.customthermoelectric.com/heatequations.html
Title: "Time Required to Cool (or heat) an Object"

There is also is a third equation on that site titled which seems to be what I actually need:
"Heat Gain (or loss) - through the walls of an insulated container "

I also found the same equation/calculator here: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatcond.html

When I did that equation it indicated that if the answer would be around 0.195 Watts I would have a Thermal conductivity of around 0.0004, which is insanely small. Apparently it's better than Aerogel - which is just nonsense. It's possible I am mixing up some numbers.
And If I had a reasonable(approximating my material insulation properties) thermal conductivity (eg. 0.035) it would amount to ~15Watts. This result is in the same ballpark as other equations that use a reasonable approximation of my insulation properties.

So I don't understand how is the 0.195W/h needed to heat up that amount of air related to the other apparently correct answer of ~15Watts of insulation conduction.

I have been wrestling with this problem since creating this thread and I am really stuck. I also tried to understand your plotting solution, but it was a bit over my head. I understand how to plot $\ln{(T_0-T)}$ against $t$, but I fail to understand how to make $\frac{1}{WC_pR}$ work in that regard.

So any clarification on these problems would be extremely appreciated.

Thank you in advance!

The basic equation is going to be:
WC_p\frac{dT}{dt}= \frac{(T_0-T)}{R}=Q
where T is the temperature of the gas in the box, T₀ is the outside temperature, t is time, W is the mass of gas in the box, C_p is the heat capacity of the gas, and R is the lumped resistance to heat transfer through the walls of the box and to the outside.

In order to do what you want to do, you need to determine R. There are two ways of doing this:

1. Use the geometry of the walls and the thermal conductivities of the walls to calculate R. The calculation must also include the convective heat transfer resistance between the outside wall of the box and the surrounding air.

2. Use your experimental data to determine the value of R.

Once you know R, you can determine the heat loss rate Q.

Since you have actual experimental data on the heating, the preferred method is method 2.

The solution to the heat transfer equation for the temperature inside the box is:

\frac{(T_0-T)}{(T_0-T_{initial})}=e^{-\frac{t}{WC_pR}}
or equivalently
\ln{(T_0-T)}=\ln{(T_0-T_{init})}-\frac{t}{WC_pR}
So you make a plot of $\ln{(T_0-T)}$ versus t, and the slope is $\frac{1}{WC_pR}$. The easiest way to do this is to use a semi-log plot.

Chet

 

[Chestermiller]

You also need to take into account the thermal inertia of the box itself (WC_p). It is probably a lot higher than the thermal inertia of air in the box. What is the weight of the box, and what is the average heat capacity of the materials comprising the box. So, in the equation, WC_p should really be that of the box, and not the air in the box.

Don't worry about the thermal conductivities and heat transfer coefficients. You have experimental data that trumps all that. Like I said, plot (T₀-T) vs t on semilog paper (or using a graphics package or a spreadsheet like Excel). Why haven't you done that yet? You should get a straight line. From the results on the graph, you should be able to accurately determine the rate of heat loss for any temperature difference between the inside of the box and the outside.

By the way, there's no such units as W/h. That should be Joules/hr. And the equation you wrote assumes that the rate of temperature rise is constant, and the temperature rise takes place over exactly an hour. Is this what your data says?

Chet

 

[Kalkunipraed]

You also need to take into account the thermal inertia of the box itself (WC_p). It is probably a lot higher than the thermal inertia of air in the box. What is the weight of the box, and what is the average heat capacity of the materials comprising the box. So, in the equation, WC_p should really be that of the box, and not the air in the box.

Don't worry about the thermal conductivities and heat transfer coefficients. You have experimental data that trumps all that. Like I said, plot (T₀-T) vs t on semilog paper (or using a graphics package or a spreadsheet like Excel). Why haven't you done that yet? You should get a straight line. From the results on the graph, you should be able to accurately determine the rate of heat loss for any temperature difference between the inside of the box and the outside.

By the way, there's no such units as W/h. That should be Joules/hr. And the equation you wrote assumes that the rate of temperature rise is constant, and the temperature rise takes place over exactly an hour. Is this what your data says?

Chet

I plotted it in Matlab before I wrote my previous post. And yes, It was basically straight. The 5C/1hour was an excerpt from the whole dataset (plotted in the first post).

You gave me much to work with. Thank you, I will try to crack it tomorrow.