TameTroll
- 5
- 0
Hello, good people -- Flagpole rigidity questions
Tis about my finals answers :) I just want to know if I'm right or not.
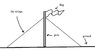
I was required to determine features of a flag pole that would enable it to withstand strong winds.
Among them are:
*String tension of strings attached to the flag pole. I answered high, naturally.
*Density of the pole. I answered high.
Reasoning: Higher density would equal more weight, so more downward force. Therefore it would need winds of stronger force to topple it.
Flexibility of the pole. I answered high.
Reasoning: If th pole has a high degree of flex, when exposed to strong winds, it will bend at the top, then return to being upright. A rigid pole will lean in its entirety and topple.
Tis about my finals answers :) I just want to know if I'm right or not.
I was required to determine features of a flag pole that would enable it to withstand strong winds.
Among them are:
*String tension of strings attached to the flag pole. I answered high, naturally.
*Density of the pole. I answered high.
Reasoning: Higher density would equal more weight, so more downward force. Therefore it would need winds of stronger force to topple it.
Flexibility of the pole. I answered high.
Reasoning: If th pole has a high degree of flex, when exposed to strong winds, it will bend at the top, then return to being upright. A rigid pole will lean in its entirety and topple.
Last edited: