[HELP] Equilibrium of Non - Concurrent Force System

[MrMechanic]

Homework Statement

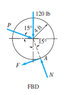
Calculate the force P that is required to hold the 120lb roller at rest on the rough incline. (see attachments for Free body diagram)

Homework Equations

Summation of Forces X = 0
Summation of Forces Y = 0
Summation of Moment along A = 0
Moment = Fd

The Attempt at a Solution

well here's what i did...
Summation of moment along A = 0 [clockwise = positive]
-4(Psin15) + 4Pcos15 - 4(120sin15) = 0
P = 4(120sin15) / 4cos15 -4sin15
P = 43.923 lb
Which is wrong.. I've found out that the correct answer is 53.6lb
Can someone explain to me? on where did I go wrong.

 

[BvU]

I understand the contribution of mg sin(15) and it gives me an idea of what you mean with A=0.
What is the component of P that has to counteract this ? I would expect some other angle to come in there.

 

[MrMechanic]

Do you mean Px and Py forces?

 

[BvU]

Well, whatever. What is your coordinate system ?
How is it possible that you can have Psin(15) and Pcos(15) in one and the same summation?
I figured the expression was a torque = 0 relationship because F and N do not appear.
That's fine. It means the summation of forces = 0 relations aren't really relevant equations, right?

 

[PhanthomJay]

If you are breaking up P into its x and y components and then summing torques about A, you are not calculating torques correctly. It is simpler to use the cross product rule for finding the torque of P about A.

 

[MrMechanic]

Well I've tried this
P = 4(120sin15) / 4sin30
P = 62.12lb
still not yet the correct answer. I really need help on this problem.

 

[PhanthomJay]

Well I've tried this
P = 4(120sin15) / 4sin30
P = 62.12lb
still not yet the correct answer. I really need help on this problem.

You have calculated the torque of the roller's weight about A correctly. But you are struggling to calculate the torque of P about A. You should familiarize yourself with the numerous ways to calculate torque. One way is to use the cross product definition: torque = (r)(P)(sin theta), where r is the length of the position vector from the point of application of P to A ( that is, 4 ft.), P, staring as itself, is the force you are trying to find, and theta is the interior angle between the force vector and the position vector. You need to determine that angle. Try again.

 

[MrMechanic]

@PhantomJay
do you mean...
torque = 0
0 = 4Psin15 -120sin75
its still incorrect.. damn I am losing my composure.. Hahaha

 

[MrMechanic]

And how do i find the interior angle between the force vector and the position vector..
Thanks for helping again..

 

[PhanthomJay]

And how do i find the interior angle between the force vector and the position vector..
Thanks for helping again..

Regarding the torque from the weight, the interior angle between the weight vector and position vector r is 15 degrees, right? Now for the torque from P, you might want to put the tail of the force vector P at the center of the roller , you know, keep it parallel just slide it down. Now can you get the angle between P and r vectors? A little geometry, that's all.

 

[BvU]

Getting there. Will you guys be careful with torque? clockwise = positive won't do! Phantom should have told you that torque is a vector. Its magnitude is as he says and its direction is perpendicular to both $\vec r$ and $m \vec g$. Whether it's +z or -z is awkward for many people, especially those who define a left-handed coordinate system. Torque is defined as $\vec r \times \vec F$. Turn $\vec r$ to $\vec F$ and follow the cork screw (in right-handed coord system e.g. x+ = down along slope, y+ is up $\bot$ slope, z+ = "into paper".

ps I can't see the 53.5 popping up. You sure it's right? My fault?

 

[PhanthomJay]

Getting there. Will you guys be careful with torque? clockwise = positive won't do! Phantom should have told you that torque is a vector. Its magnitude is as he says and its direction is perpendicular to both $\vec r$ and $m \vec g$. Whether it's +z or -z is awkward for many people, especially those who define a left-handed coordinate system. Torque is defined as $\vec r \times \vec F$. Turn $\vec r$ to $\vec F$ and follow the cork screw (in right-handed coord system e.g. x+ = down along slope, y+ is up $\bot$ slope, z+ = "into paper".

ps I can't see the 53.5 popping up. You sure it's right? My fault?

i don't get the book answer either. Good point on signage.
If cw is plus, ccw is minus.

 

[MrMechanic]

Same here.. I've tried lots of different ways to solve for P... And I still can't find a way on how this is done...
What if i sum forces along y. and along x all = 0. Will i still get P? there are three unknowns. N,F, and P. All I need is P. And i still don't get the 3D system. We are just only tackling 2D forces. I have yet to learn those lessons. And by the way thanks again.. I'll try again.

 

[PhanthomJay]

This is a 2D problem not 3D.
Stop trying to match the ' book ' answer and solve for P. I have already given you a couple tips.

 

[BvU]

Agree with Phantom. Balancing only two of the (projected) forces to get |torque|=0 is sufficient here. You didn't need N and F when you chose A as reference point for the torque. Don't need them now, either. Two worries less.

Can we now please get you to take a look at the angles? You projected mg on a line along the slope using 15 degrees. Good. What angle does P make with this same line ? That is really all.

By the way, I have great difficulty imagining what F is and where it comes in. Was it in the original OP or is it only in your rendering thereof?