[Help] Genus: Having difficulty to fully understand it.

  • Context: Undergrad 
  • Thread starter Thread starter probiner
  • Start date Start date
  • Tags Tags
    Difficulty
Click For Summary

Discussion Overview

The discussion revolves around the mathematical concept of genus, particularly in relation to surfaces and their characteristics. Participants explore the definition of genus, its visual representation, and its implications in modeling programs. The conversation includes theoretical aspects, practical examples, and personal interpretations of the concept.

Discussion Character

  • Exploratory
  • Technical explanation
  • Conceptual clarification
  • Debate/contested

Main Points Raised

  • One participant expresses confusion about the concept of genus, particularly when handles or holes share space, and seeks clarification on the rules governing these numbers.
  • Another participant explains that in the theory of Riemann surfaces, genus relates to the number of cuts that can be made without disconnecting the surface, providing examples of a sphere and a torus.
  • A participant suggests that the genus can be understood as the number of exits minus one, summed over each connected piece, and notes that this generalization may differ from the usual definition of genus.
  • One participant humorously acknowledges their understanding of genus has shifted from thinking of it in terms of holes/handles to thinking of it in terms of cuts.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the definition and implications of genus, with multiple interpretations and models presented. The discussion remains unresolved regarding the precise relationship between genus, holes, handles, and cuts.

Contextual Notes

There are limitations in the discussion regarding the definitions of genus, as participants express differing views on how to calculate or visualize it, particularly in complex cases where holes or handles interact.

probiner
Messages
10
Reaction score
0
Hi
I'm having trouble to fully understand the concept of Genus: https://en.wikipedia.org/wiki/Genus_(mathematics)

Those examples are preety simple to me Genus = number of handles/holes. But what the wikipedia doesn't cover (at least visually) is when these handles or holes share space like in the last 3 examples of the image below:

Genus_.png


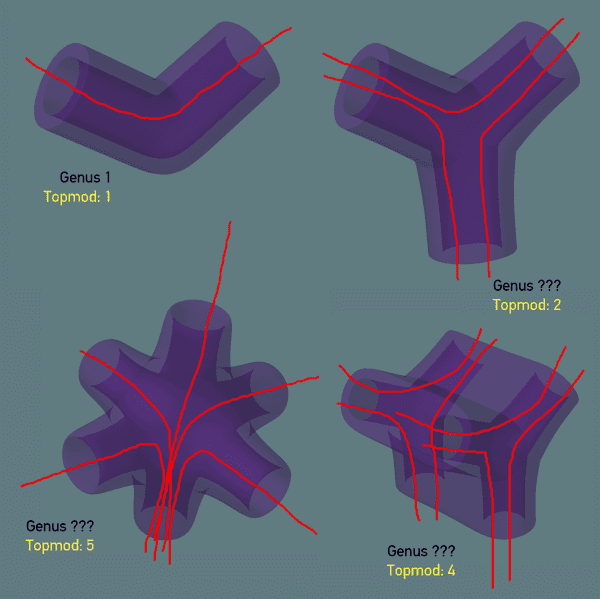
TopMod is a modeling program that has a display that shows how many Genus the present mesh has.
I was expecting different numbers honestly...

I can't get a rational grasp to understand the rules of these numbers.
http://forums.newtek.com/images/smilies/brians/help.gif

It seems that it's the number of possible exits there is when going through a hole of the mesh.
So the Single Y shape has Genus 2 because when I go through Hole-number-1 I can exit on Hole-number-2 or Hole-number-3, so 2 possibilities.
The Double Y shape has Genus 4 because it's the previous situation but independent and doubled.
Is this it?

Cheers
 
Last edited by a moderator:
Physics news on Phys.org
In the theory of Riemann surfaces, the genus is the number of cuts along closed circles that can be made on the surface without disconnecting it into two separate pieces.

On a sphere, any cut will disconnect it so its genus is zero. On a torus, a cross sectional cut will not disconnect it but rather, turn it into a cylinder but a second cut will disconnect it. So its genus is 1.

A couple of your pictures are what happens to the surface after the cuts are made. those are the two with and even number of exits. they come from surfaces of genus 1 and 3.

In your pictures, the genus just seems to be the number of exits minus 1 ,summed over each connected piece. This idea of genus seems to provide a way to generalize the idea of genus used for Riemann surfaces. the genus is the number of exits. But for a surface of usual genus 2, this generalized genus will be 3 instead.
 
Last edited:
Thank you for the clarification, it made my head become a Genus 2 (Open mouth smiling and ear canals :D)
Replacing in my brain Genus = holes/handles by Genus = Cuts.

Cheers
 
Last edited:
Oh by the way I was having a bit of hard time of seeing the Homeomorph between them but here it is:
Homeomorph3.gif
 
Last edited:

Similar threads

Undergrad A way to comprehend the geometry of a hypercube
  • · Replies 2 ·
Replies
2
Views
2K
On the cusp of fully grasping Method of Characteristics
  • · Replies 1 ·
Replies
1
Views
3K
Depth of NPT Holes: How to Fully Screw in Fittings Roy's Q&A
  • · Replies 8 ·
Replies
8
Views
11K
Undergrad How Does Special Relativity Affect Perceptions of Simultaneity?
  • · Replies 32 ·
2
Replies
32
Views
3K
Undergrad Two recent tests of loop quantum gravity theory
  • · Replies 15 ·
Replies
15
Views
6K
Graduate ± sqrt(b^2 - a^2) = ± b ± ai ?
  • · Replies 6 ·
Replies
6
Views
3K
A few questions about airflow and filters...
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Help me understand skewness in QQ-plots please
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Time travel is a fact or fiction.?
  • · Replies 9 ·
Replies
9
Views
3K
Insights Fermat's Last Theorem
  • · Replies 105 ·
4
Replies
105
Views
10K