Help Needed: Last Physics Lab Assignment Rod Problem

[riseofphoenix]

I need to get a 100 on this last Physics lab assignment, but I can't get this "rod"

...problem :(
Help would be appreciated

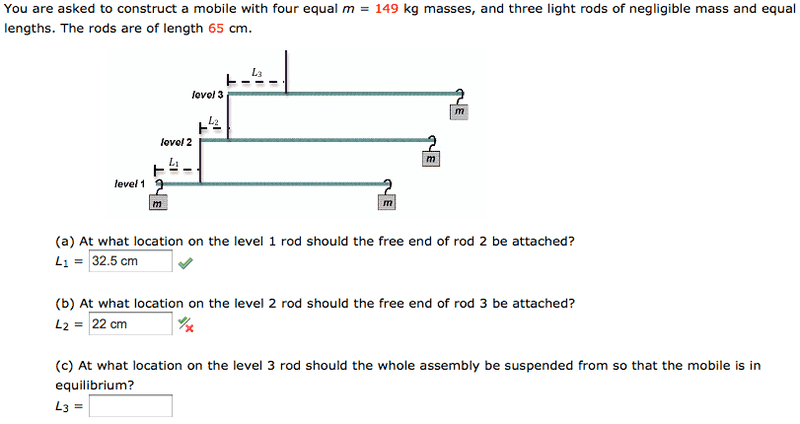
(a) L₁ = (65 cm)/2 = 32.5 cm

"CORRECT"

(b) [(149 kg)(1) + (149 kg)(65 cm) + (149 kg)(65 cm + 32.5 cm)] / (3)(149 kg)
= (149 + 9685 + 14527.5) / (447)
= 54.5

Then,

54.5 - 32.5 = 22 cm

"INCORRECT"

-.- Help?

(c) ?

L3 _________

 

[superdave]

What's the force the string from 1 exerts on 2, and where is that force applied?

 

[riseofphoenix]

What's the force the string from 1 exerts on 2, and where is that force applied?

(149)(65)? in the vertical direction.

 

[superdave]

(149)(65)? in the vertical direction.

Well, that's torque. I just want to know if you held the string with rod 1 and its masses attached, instead of attaching it to the rod, how much force would be pulling down on your hand (ignoring the weight of your own hand)?

 

[riseofphoenix]

well, that's torque. I just want to know if you held the string with rod 1 and its masses attached, instead of attaching it to the rod, how much force would be pulling down on your hand (ignoring the weight of your own hand)?

149(9.81)?

 

[superdave]

149(9.81)?

aren't there 2 masses on rod 1?

 

[riseofphoenix]

aren't there 2 masses on rod 1?

Oh...
(149+149)(9.81)

 

[superdave]

Oh...
(149+149)(9.81)

Okay, now we can ignore 9.81 because it will be in every term.

But my point is, you can model rod 2 as having 1m (149 kg) at one end and 2m (298 kg) at the other.

So find the center of mass of that system for Rod 2.
Rod 3 can be modeled in a similar way, but you now have 3m on one end.

 

[riseofphoenix]

Okay, now we can ignore 9.81 because it will be in every term.

But my point is, you can model rod 2 as having 1m (149 kg) at one end and 2m (298 kg) at the other.

So find the center of mass of that system for Rod 2.
Rod 3 can be modeled in a similar way, but you now have 3m on one end.

[(149 kg)(1 m) + (298 kg)(2 m) + (447 kg)(3 m)] / (3 m)(447 kg)

Like that?

 

[superdave]

Eep, no. m as in m=mass=149 kg.

Rod 3 has 3*149 kg at one end, and 149 kg at the other. Because all of rod 2 and rod 1's mass (a total of 3*149 kg) is supported by one string at the end of rod 3.

 

[riseofphoenix]

Eep, no. m as in m=mass=149 kg.

Rod 3 has 3*149 kg at one end, and 149 kg at the other. Because all of rod 2 and rod 1's mass (a total of 3*149 kg) is supported by one string at the end of rod 3.

Ok so the equation should be...

[(149 kg)(1) + (149 kg)(65 cm)(2) + (149 kg)(65 cm + 32.5 cm)(3)] / (3)(149 kg)??

Like that?

 

[superdave]

No, it should be the mass*distance at the one end + mass times distance at the other end, divided by total mass.

Or [149 kg * (3) + 149 kg *(1) * 65 cm] / 4 * 149kg

the diagram shows that L₃ is the distance from the end of that rod to the balance point, so you don't need to add anything.

If you do the algebra, you should find that because the masses are equal, if you have 3 on one side and 1 on the other, the balance point is just 1/4 L. for rod two, it's 1/3 L. So you kind of stumbled into the answer the wrong way.

 

[riseofphoenix]

[149 kg * (3) + 149 kg *(1) * 65 cm] / 4 * 149kg


^

That still doesn't give me the right answer though :(
I just submitted 17 cm and it still marked it as incorrect!

I did:

447.0000 + 9685.0000 / 596.0000

10132.0000 / 596.0000

17.0000

?

 

[superdave]

You are right, my bad. The first term is at 0 cm. So

[149 kg * (3) * 0 cm + 149 kg *(1) * 65 cm] / 4 * 149kg

 

[riseofphoenix]

You are right, my bad. The first term is at 0 cm. So

[149 kg * (3) * 0 cm + 149 kg *(1) * 65 cm] / 4 * 149kg

I did

0 + 9685.0000 / 596.0000

= 16.2500

I put 16.25 cm in the answer box and I still got it wrong :(
I've already used 3 submissions...anything beyond 4 with be .33 points off :(

 

[superdave]

this is part c, right?

If 16.25 cm isn't the answer to part c, then I have no idea what's going on.

 

[riseofphoenix]

This is part c yeah...

 

[riseofphoenix]

wait no this is part b!

 

[riseofphoenix]

ohh you were doing part c?

 

[riseofphoenix]

oh 16.25 for part c is CORRECT nvm...

I was asking for part b

 

[superdave]

Oooh. Put that answer in part C to make sure my reasoning is correct. If it is, then part b should be:

(0cm * 2 * 149 kg + 65 cm * 149 kg * 1) / 3 * 149 kg.

 

[riseofphoenix]

this is part c, right?

If 16.25 cm isn't the answer to part c, then I have no idea what's going on.

16.25 cm IS the answer to part c, sorry...
I thought we were doing part b because that's what I was having trouble on.

 

[riseofphoenix]

You are right, my bad. The first term is at 0 cm. So

[149 kg * (3) * 0 cm + 149 kg *(1) * 65 cm] / 4 * 149kg

Ok, so part b should be 21.67 right?

 

[superdave]

Ok, so part b should be 21.67 right?

It should be.

 

[riseofphoenix]

It should be.

Awesome! They're all right.
Thanks a bunch!

 

[superdave]

To be sure understand it:

The locations of the masses on the rod below don't matter. All the total mass in all of the rods below (really all the weight) is in the string at the end of the current rod.

For rod b, you have 149*2 kg at x=0 cm. And 149 kg at x=65 cm. Divide by total mass (149 kg * 3).

For rod c, you have 149 kg * 3 at x=0 cm. And 149 kg* 1 at x = 65 cm. Divide by total mass (149 kg * 4).