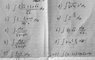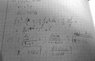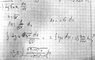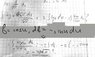Help with IntegralS Very Important Quick

[Student from UA]

Hi! I`m poor student from Ukraine! I`m writing u becouse u are my last chans!
So I need to do homewofk for monday-tuesday. I have problem becouse i was ill and siting at home during lessons about integration! Sorry for My bad English, but i hope u understad.
So i have 10 integrals! At first i search in intarnet some calcus. I found www.cal101.com But it give me only result. Function step by step only for money! But i haven`t! what i must do? =( Thanks God and Google I find U.
I hope u help me becouse it`s very very important to me.
So 10 integrals(all indefine):
1) (2*(x^(1/3))+3*x*(x^(1/2)))/(x^(1/4))
2) ((x^3+1)^(1/4))*(x^2)
3) (1-2*sinx)/(cosx^2)
4) 2^(x/2)
5) dx/((4-x^2)^(1/2))
6) tg(x^(1/2))*(dx/x^(1/2))
7) dx/((4+x^2)^(1/2))
8) (sin(x/2))^2
9) lnx/(x^(1/2))
10) (1-3x)cos2x
They are in Attach Files!

 

[cristo]

Hi and welcome to the forums. Firstly please note that the forum rules state that you must show some work before we can help. What do you know about integration? Have you had a go at any of the questions?

Also, in future, please note that we have homework forums specifically for these type of question.

 

[Student from UA]

Hi and welcome to the forums. Firstly please note that the forum rules state that you must show some work before we can help. What do you know about integration? Have you had a go at any of the questions?

Also, in future, please note that we have homework forums specifically for these type of question.

I agree with u, - I must do homework not u. I`ve just start so in atach u can see 1 an 2 . But i think it isn`t right/

 

[cristo]

1. x\sqrt{x}=x\cdot x^{1/2}=x^{3/2}

2. Your technique is incorrect. Have you come across integration by substitution? Try the substitution y=x^3+1

 

[Student from UA]

U know if i weren`t ill all 2 week, i do home work well. I`m have good marks 87 of 100. I have never ask people to help me in algebra.. butt know. very X situation. I haven`t free time to learn intaegrals, becouse now i do years work in Descrete Mathematic. =( Next week i must to complete. Thanks God with Descrete mathematica i`m good.

 

[Student from UA]

1. x\sqrt{x}=x\cdot x^{1/2}=x^{3/2}

2. Your technique is incorrect. Have you come across integration by substitution? Try the substitution y=x^3+1

O fu... Really. It`s child mistake... Oh... Sorry. Hm . I`m trying again.

 

[cristo]

Ok. Don't worry, and don't let youself get stressed; it's only homework, not a life and death situation! Try and calm down a little, and take your time. Then you're less likely to make mistakes.

 

[Student from UA]

About 1. I`m stuck in a middle. I have result (72x^(13/12))+(52x^(9/4)))/39. Is it right?
About 2. I don`t under stand explain me please.

 

[Student from UA]

You know i do right the 1st =) I compare it with cal101 result. Cal101 make other version but in result we have right rsult =) He he I love integrals!

 

[Student from UA]

But.. Remain else 9 . What to do?

 

[Student from UA]

ANd u now... U have 3 pm. But i`m in 0.13 AM =( Really want go to sleep but How? =( when i think, what will hapen with me if i will not complete the task...

 

[Student from UA]

About the 2. In calc101.com result (atach file) diferent only with x^3 (see my version) . So where i do mistake , and in the and have misterios x^3

 

[Crosson]

How did you get in this bad situation?

 

[Student from UA]

I much powerfully was ill, and has missed nearly 2 weeks lessons. Beside me was a temperature from 35.6 before 39. ANd i couldn`t do anything.

 

[cristo]

Right: question 1. \int\frac{2x^{1/3}+3x^{3/2}}{x^{1/4}}dx=\int 2x^{1/2}+3x^{5/4} dx Can you integrate this using the rule for fractional powers?

question 2. \int(x^3+1)^{1/4}x^2 dx.
Are you familiar with the method of substitution? If so use the substitution y=x^3+1; this gives dy=3x^2dx. Substituting into the integrand gives \int y^{1/4}\frac{dy}{3}. Can you solve this? The substituting in for x will give you the solution.

 

[cristo]

A few more hints for the ones I can see how to do immediately!

5&7 will be some trig subsitutions. For 5 let x=2sinu, for 7 let x=2tanu.
8. looks like it will be do-able using the double angle formula to express it in terms of sinx (or cosx)
10. use integration by parts.

That should give you a bit to work on, I'll have a look at the others in more detail when I've got time [or if anyone else is reading, feel free to help, of course!]

 

[Crosson]

How much do you know about integration?

 

[Student from UA]

To Crosson:
Not much. =(. But I trying to rescue the situation.
I`ve just get up. Now i start to do the second. And when i finish it, try to make 5&7.

 

[Student from UA]

THX . I `ve done the second! Integration is interesting ... but.. now i just start to do 5... =9

 

[Student from UA]

Hm see the 5. I can`t stand, what i do wrong. help

 

[Student from UA]

Hm.. how u get 2sinudu ? if x=2sinu.

 

[Student from UA]

dx=-2cosudu.

 

[cristo]

Hm.. how u get 2sinudu ? if x=2sinu.

You use the chain rule: dx=d(2sin u)=2 cosu du.

[Sorry, above I said that your notation d(2sin u) was not correct. Of course, it is correct, but not all that useful here!]

 

[Student from UA]

He. the 8 i `ve done for 20-40 sec. =) see in atach

 

[Hootenanny]

The correct integral should be something like;

x = 2\sin(u) \Rightarrow dx = 2\cos(u) \; du

\int\frac{dx}{\sqrt{4-x^2}} = \int\frac{2\cos(u)}{2\sqrt{1-\sin^2(u)}}du

Which should be somewhat easier to integrate.

Edit: Damn beaten to, you get up too early in the morning cristo!

 

[Student from UA]

so how i must write in copy book about the 5 ? how u get 2sinudu can u write?

 

[Student from UA]

The correct integral should be something like;

x = 2\sin(u) \Rightarrow dx = 2\cos(u) \; du

\int\frac{dx}{\sqrt{4-x^2}} = \int\frac{2\cos(u)}{2\sqrt{1-\sin^2(u)}}du

Which should be somewhat easier to integrate.

Edit: Damn beaten to, you get up too early in the morning cristo!

\int\frac{dx}{\sqrt{4-x^2}} = \int\frac{2\cos(u)}{2\sqrt{1-\sin^2(u)}}du = \int\1du=u+c And what to do?

 

[cristo]

Edit: Damn beaten to, you get up too early in the morning cristo!

Yea, that's true, but I made a rather stupid mistake. I've deleted my incorrect post, to avoid confusion.

Student: Look at Hootenanny's post for qn 5.

 

[Hootenanny]

\int\frac{dx}{\sqrt{4-x^2}} = \int\frac{2\cos(u)}{2\sqrt{1-\sin^2(u)}}du = \int\1du=u+c And what to do?

Well, you were given the integrand in terms of x, but now we have an integral in terms of u. So the next step would be to change the integral from a function of u back to a function of x.

 

[Student from UA]

Well, you were given the integrand in terms of x, but now we have an integral in terms of u. So the next step would be to change the integral from a function of u back to a function of x.

U know... I know that. I don`t know how to do that! =(

 

[Hootenanny]

U know... I know that. I don`t know how to do that! =(

Don't let yourself get stressed out when your answering questions, after all they're only questions. Take a look at the first line in one of my previous posts;

x = 2\sin(u) \Rightarrow dx = 2\cos(u) \; du

Does this give you any ideas?

 

[Student from UA]

sin(u)=x/2
u=((-1)^n)arcsin(x/2) + Pi n, n E Z

 

[Hootenanny]

sin(u)=x/2
u=((-1)^n)arcsin(x/2) + Pi n, n E Z

Your almost correct, but aren't you forgetting one 'little' thing...? I'm impressed at how your represent your solution, not many students would think of representing it this way; in truth it is not normally scary unless the question explicitly requires it.

 

[Gib Z]

I don't understand why you think that. Good to notice you've learned latex so fast.
\sin u = \frac{x}{2}
\arcsin (\sin u) = \arcsin (x/2)
u=\arcsin \frac{x}{2}

I see why you wrote it that way, but it over complicates the situation this time. Quite Interesting though...

EDIT: In fact it destroys you in this case...The pi*n term gets included in the constant term, and then the integral becomes (-1)^n \arcsin (x/2) + C, and that is incorrect...

 

[Student from UA]

I start do 6th and.. have problems in middle. see in atach

 

[Student from UA]

so the rsult of 5: \intdu=\arcsin \frac{x}{2} + C ?

 

[Gib Z]

I have no idea what the "tg" is, but I deduce its the tangent function.

Even if it isnt, let u=\sqrt{x} Then \frac{du}{dx} = \frac{1}{2u}, dx = 2u du

so the integral becomes

\int \tg u \frac{2u}{u} du = 2\int \tg (u) du

EDIT: As to post 36, q5, yes that is the answer. The reason you can not write it as you did previously is because it is only valid for n E Z, but we need it to be valid for all real values of n.

 

[Student from UA]

Gibs u=\sqrt{x}
du=\frac{1}{2\sqrt{x}}dx then dx=2\sqrt{x}du

 

[Gib Z]

Check your typing, you forgot to use the right hand brace } instead of right breacket ). Anyway, then you are correct. However, didn't we say u=\sqrt{x}?

 

[Gib Z]

You know either way it doesn't matter. You are stuck with
2\int \frac{\sin x}{\cos x} dx which can be solved by letting u = cos x

 

[Student from UA]

right result?

 

[Gib Z]

Nope.

2\int \frac{\sin x}{\cos x} dx
let u = cos x, then du = - sin x dx
-2\int \frac{1}{u} du = -2\log_e u + C = -2 \log_e (\cos x) + C

 

[Student from UA]

Nope.

2\int \frac{\sin x}{\cos x} dx
let u = cos x, then du = - sin x dx
-2\int \frac{1}{u} du = -2\log_e u + C = -2 \log_e (\cos x) + C

U right, i agree with u. I made a child mistake =(
simply I sit near computer and do homework already 6 hours and have square head

 

[Student from UA]

start the 7th. Stop in the middle. See in atach. :zzz:

 

[cristo]

So you have the integral of sec u= 1/cos u. To compute this, try multiplying top and bottom by sec u+tan u.

 

[Student from UA]

i don`t understand u cristo =(

 

[Student from UA]

stop don`t tell me anything 5 minut i try tio solve it again.

 

[Student from UA]

secu^2= 1+tgu^2 => secu=sqrt(1+tgu^2)
so compare 3rd step and last in atach . hmm

 

[cristo]

\sec u=\sec u\cdot\left(\frac{\sec u+\tan u}{\sec u+\tan u}\right). Can you integrate this?

[Hint: How is the numerator related to the denominator?]

 

[Student from UA]

ou... sorry =) how to delete... -) it`s mistake