Help with Optics: Calculate Maximum Angle of Incidence

[stunner5000pt]

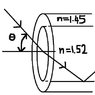
Ok have a look at the diagram

The diagram shows the end of an optical fibre. Inside is the core of n = 1.52 and the outer covering is the caldding n=1.45. For sufficiently small angles teh incident rays will be guided by the fiber and remain in teh core due to internal reflection. What is the maximum angle of incidence (theta) for which the light transmitted across the boundary will remain in the core??

I cn find the critical angle for which teh light will stay in teh core (i.e. the boundary of the core and the cladding) and that angle is 72.5 degres

so the angle the light inside the fiber must not exceed 17.5 degrees w.r.t. the base of the lining of the cladding.
So drawing some parallel lines the transmitted angle (refracted angle) into the core must not xceed 17.5 degrees
thus n_{1} sin \theta_{1} = n_{2} sin \theta_{2}
since it is being transmitted from air to the core as the diagram shows

1 sin theta = 1.52 sin 17.5
theta = 27 degrees. So the angle of incidence must not exceed 17.5 degrees? Is this good ??

 

[thepatientmental]

Yes, your calculation is correct. The maximum angle of incidence for the light to remain in the core is 17.5 degrees. This is also known as the acceptance angle of the optical fiber. Any angle greater than this will result in the light being transmitted out of the core and into the cladding, leading to loss of signal. It is important to ensure that the angle of incidence does not exceed this value in order to maintain efficient transmission of light through the fiber. Good job on your calculation!