Help with simple resistor problem

[Mr. Hiyasaki]

SEE POST 4
​

I am having problems solving these resistor problems and was wondering if anyone could help. Really what I think my problem is is that i don't know what to do if there are series and parallel resistors on the same circuit

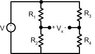
For attachment three The resistance of the entire circuit and RL are supposed to be equal to each other and then you are wanting to find the resistance of R to make that true. The actual problem used RAB = RL = 625. ohms. and you are supposed to get 361 for R, but my numbers are all over the board and i can't hit that, because i don't know what to do with the resistor inbetween the 2 parallel resistors.


then for attachment 6.jpg if i know the voltage of the circuit and the ohms of the resistors i am supposed to find the current.
In the practice problem i am trying to find out my numbers are
If the resistances R1= 44. ohms, R2 = 14. ohms, and R3 = 26. ohms, and the voltage V = 6.0 volts, what is the current ix (in Amperes) in the circuit.

The answer i am given is 4A, but i keep coming up with .11

​

 

[chroot]

In your first circuit, begin by combining resistances.

Notice that RL is in series with the R above it. Combine those into one resistor, R + RL. Redraw the entire circuit, this time with only one resistor where there once was two, if it'll help you understand.

Next, notice that the combined (R + RL) resistor is in parallel with the middle R. You can combine those as:

\frac{1}{\frac{1}{R} + \frac{1}{R + R_L}}

Next, notice that that combination itself is in series with the final R...

In this way, you'll combine all the resistances into one equation, which you can then solve for R.

- Warren

 

[chroot]

The second problem is done the same way. Combine parallel and series resistors until you have the equivalent resistance of the entire circuit, then calculate the total current with Ohm's law. Next, since you know all that current is flowing through R1, you know the voltage drop across R1. Next, since you know the voltage drop across R3, you know the current through R3.

- Warren

 

[Mr. Hiyasaki]

thanks a whole lot, i think i am starting to understand this stuff. I wish the problems were a little simplier then worked their way up, but I don't have that choice. THank again for the help.


I have two more questions if someone wouldn't mind helping me out a bit with these as well

For the first one, I am supposed to find Vx. And I don't really understand it at all.


Then the second one (attach 9.jpg) I am supposed to find the error in measuring the current flowing through r1 with an ammeter with internal reistanc of .1 ohms. Would adding the resistance of .1 ohms to r2 as a series, then caculate the total resistance and find the current, and then subtact that from the current of the circuit without the ammeter be correct?

 

[SGT]

thanks a whole lot, i think i am starting to understand this stuff. I wish the problems were a little simplier then worked their way up, but I don't have that choice. THank again for the help.


I have two more questions if someone wouldn't mind helping me out a bit with these as well

For the first one, I am supposed to find Vx. And I don't really understand it at all.


Then the second one (attach 9.jpg) I am supposed to find the error in measuring the current flowing through r1 with an ammeter with internal reistanc of .1 ohms. Would adding the resistance of .1 ohms to r2 as a series, then caculate the total resistance and find the current, and then subtact that from the current of the circuit without the ammeter be correct?

The resistors R1 and R2 are in series and so are R3 and R4. You can calculate the currents through each series connection. Knowing the currents, you can calculate the voltage drops in R2 and R4 and finally Vx.
For the second circuit your approach is correct.