- #1
NIZBIT
- 69
- 0
This stuff is making me bang my head against the wall. I understand the concept and notation of summation with no problems. It seems though for about every one problem I get right there is five I get wrong. The only thing I can think I'm doing wrong is bad algebra habits or I'm using the summation properties and formulas at wrong times. I know I could work these problems the long way, but I'm missing the point of the lesson. Could someone please let me know what I'm doing wrong? Here is one I got right:
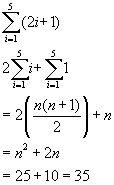
Here is one I got wrong:
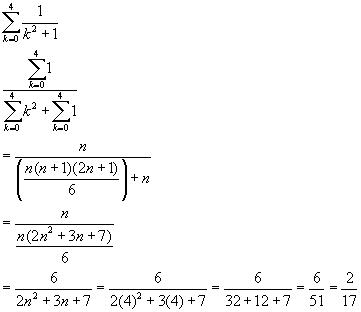
Here is one I got wrong:
 . I think this might be the problem I'm having. It would also explain why I'm getting so few right. Both the book and my teacher led me to believe that I can use those forumals to solve ANY problem.
. I think this might be the problem I'm having. It would also explain why I'm getting so few right. Both the book and my teacher led me to believe that I can use those forumals to solve ANY problem.