Holding down steel plate w/ multiple magnets: Does orientati

AI Thread Summary
The discussion focuses on using an array of Neodym magnets to secure a steel plate on a 3D printer's heated aluminum bed. Two orientations of the magnets are compared: one with all magnets aligned and another with every second magnet flipped. The goal is to ensure the steel plate remains flat and stable, preventing movement in the XY direction. The flipped orientation is suggested to be more effective if the distance between the magnets and the steel plate is smaller than the distance between the magnets, as it enhances magnetic flux and stability. Overall, the orientation of the magnets significantly impacts the effectiveness of holding the steel plate in place.
Wookbert
Messages
2
Reaction score
0
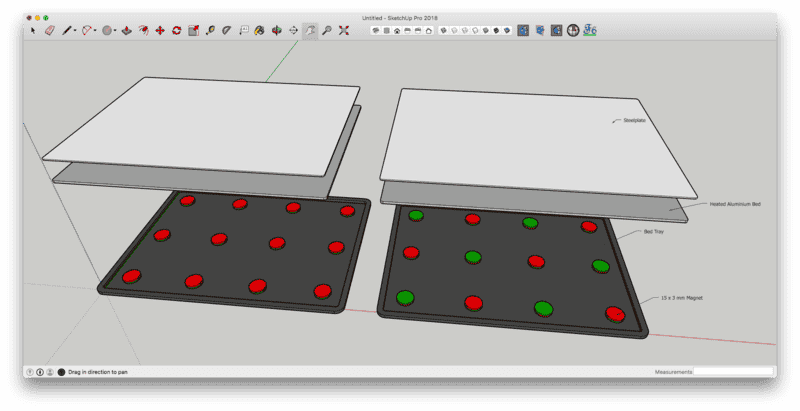
The picture below shows an image of a bed from a 3d printer, which I intend to equip with an array of 15 x 3 mm Neodym magnets to hold down a steel plate. The steel plate itself is not and can not be equipped with magnets. Theres a heated aluminium bed between magnets and steel plate and the magnets are specified to withstand 150°C.

The left side shows all 12 magnet arranged with the same orientation, on the right side every second magnet is flipped. The distance between the magnet is wide enough so they don't noticeably attract/distract/disturb each other.

Question: The goal is that the steel plate lays flat (Z direction) and does not accidentally move in XY direction. Is either magnet orientation better than the other in achieving this?

Print bed magnet orientation.png
 

Attachments

  • Print bed magnet orientation.png
    Print bed magnet orientation.png
    15.8 KB · Views: 472
Physics news on Phys.org
The second one will be better if the distance between steel plate and magnets is smaller than the distance between the magnets. The second orientation provides return lines for the magnetic flux and leads to stronger induced magnetic fields in the plate.
 
Thank you!
 

Thread 'Maxwell stress tensor'

This is from Griffiths' Electrodynamics, 3rd edition, page 352. I am trying to calculate the divergence of the Maxwell stress tensor. The tensor is given as ##T_{ij} =\epsilon_0 (E_iE_j-\frac 1 2 \delta_{ij} E^2)+\frac 1 {\mu_0}(B_iB_j-\frac 1 2 \delta_{ij} B^2)##. To make things easier, I just want to focus on the part with the electrical field, i.e. I want to find the divergence of ##E_{ij}=E_iE_j-\frac 1 2 \delta_{ij}E^2##. In matrix form, this tensor should look like this...
View full post »
Thread 'Applying the Gauss (1835) formula for force between 2 parallel DC currents'

Thread 'Applying the Gauss (1835) formula for force between 2 parallel DC currents'

Please can anyone either:- (1) point me to a derivation of the perpendicular force (Fy) between two very long parallel wires carrying steady currents utilising the formula of Gauss for the force F along the line r between 2 charges? Or alternatively (2) point out where I have gone wrong in my method? I am having problems with calculating the direction and magnitude of the force as expected from modern (Biot-Savart-Maxwell-Lorentz) formula. Here is my method and results so far:- This...
View full post »

Similar threads

I Shielding behavior of a steel cuboid in a DC magnetic field
Replies
1
Views
352
Does the magnetic force affect lateral movement of a magnet on a metal plate?
Replies
5
Views
2K
Structure adding rotational stiffness to a plate
Replies
15
Views
2K
Seismic isolator based on magnetic forces
Replies
7
Views
2K
A little critique on magnetic lines of force.
Replies
1
Views
6K
Nuclear Magnetic Resonance (NMR) Explanation
Replies
4
Views
5K
Can Evolved State: Dichotomy Capture Your Imagination?
Replies
1
Views
4K
Do Movies Teach Us Realistic Life Skills?
Replies
1
Views
10K
Kerbal Space Program - Rocket Design Basics
Replies
2
Views
9K
Mathematica This Week's Finds in Mathematical Physics (Week 266)
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top