TwoEG
- 13
- 0
Homework Statement
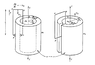
1. Circuit moves downward while cylinder magnet is fixed.
2. Cylinder magnet moves upward while circuit is fixed.
Gain emf in circuit.
Homework Equations
All those maxwell equations...
F=v x B
The Attempt at a Solution
[/B]
So first question is not that hard. Circuit moves in a static magnetic field. Okay. And I saw second question. Hmm. isn't it just relatively the same case as 1st one? But I've never thought of F=v x B in this way. I tried to see moving uniform magnetic field in fixed charge's coordinate. But it's just uniform magnetic field that doesn't change with time. And me, charge doesn't move at all from my perspective.
To sum up, my question is how does moving-uniform magnetic field is expressed in fixed charge's coordinate and how can I explain the forces that exerted upon this charge?