Ok, basically hooke's law states that within an elastic limit of a material, the Force is directly proportional to its extension, given by F = kx, where x is the extension in metres, and k is the spring constant with units [N/m].
Say, a spring has a spring constant of 360N/m, so for every 1m u compress the spring, the spring exerts a force in opposite direction of 360N.
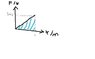
Looking at the thumbnail attached, u can see that its a force-extension graph illustrating hooke's law, with gradient of k [360N/m]. To calculate the ELASTIC POTENTIAL ENERGY stored in the spring, its Force x distance, which is the area under the graph, shaded in blue.
Therefore, Elastic Energy = 0.5Fx = 0.5(kx)x = 0.5kx2.
Assuming a spring is compressed by x metres, it contains elastic potential energy of 0.5kx2. Then following the law of conservation of energy, where all elastic potential energy is converted into kinetic energy of the ball being launched.
0.5kx2 = 0.5mv2
kx = mv2
v = sqrt(kx/m)
Hope this clarifies your doubt.