Hooke's law spring configurations

[judas_priest]

Homework Statement

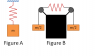
As shown in Figure A, a block of mass m is hanging from a spring attached to the ceiling. As shown in Figure B, two blocks of mass m/2 are hanging from two strings that are attached to a spring that has the same spring constant k. If the spring in Figure A is stretched a distance d, how far will the spring in Figure B stretch?2. The attempt at a solution

The problem (Figure-B)is approached based on identifying that the center of the spring acts like a fixed point and does not shift (because of symmetry). Therefore the problem now breaks down into two equal springs in series. Don't know how to approach from here. After it breaks down into two springs of equal spring constants, I used (k1k2)x/2(k1+k2) = mg/2 did this for both masses respectively. Not getting me anywhere. Anyone have a different approach or another way to look at this problem?

 

[darkxponent]

HINT: The elongation depends on tension in the spring.

 

[haruspex]

the problem now breaks down into two equal springs in series. Don't know how to approach from here. After it breaks down into two springs of equal spring constants, I used (k1k2)x/2(k1+k2) = mg/2 did this for both masses respectively.

That's not quite the point of taking the centre to be fixed. The idea is that you only have to think about one half of the spring and one mass. You can conceptually replace the other half of the system by a wall.

 

[darkxponent]

That's not quite the point of taking the centre to be fixed. The idea is that you only have to think about one half of the spring and one mass. You can conceptually replace the other half of the system by a wall.

Is that even necessary? I mean the problem can be without cutting the spring.

 

[barryj]

Make the problem simple. If the system is static, consider the spring fixed or clamped at one of the pulleys. Then compare the tension in the spring in case A with case B. What causes the tension, and how much is it? No formulas needed.

 

[judas_priest]

That's not quite the point of taking the centre to be fixed. The idea is that you only have to think about one half of the spring and one mass. You can conceptually replace the other half of the system by a wall.

But that would just give me T = Mg/2 and substituting for M from first system would give me T = kd/2. Substituting T as -kx would give me x = d/2

Is this correct?

 

[judas_priest]

Make the problem simple. If the system is static, consider the spring fixed or clamped at one of the pulleys. Then compare the tension in the spring in case A with case B. What causes the tension, and how much is it? No formulas needed.

Wouldn't the tension on both sides be same? Because the string is ideal, and hence tension is the same everywhere. Or did I not get your point right?

 

[barryj]

I can't believe you guys are making the problem so complicated. If you fix the spring at the right end, then have the same spring but with half the mass.

 

[judas_priest]

Is that even necessary? I mean the problem can be without cutting the spring.

So, what's your way of looking at it and approach to it?

 

[judas_priest]

I can't believe you guys are making the problem so complicated. If you fix the spring at the right end, then have the same spring but with half the mass.

Yup, it's quite a simple problem. Just getting back to Hooke's law after 2 years.

 

[haruspex]

I can't believe you guys are making the problem so complicated. If you fix the spring at the right end, then have the same spring but with half the mass.

My reading of the OP is that symmetry is the ordained method to be used.

 

[darkxponent]

So, what's your way of looking at it and approach to it?

For me the problem is even simpler. Just find the Tension in the spring and equating it to Kx. There is no need to fix the strung or cut the spring!

 

[judas_priest]

For me the problem is even simpler. Just find the Tension in the spring and equating it to Kx. There is no need to fix the strung or cut the spring!

That was my initial attempt. Doesn't get me to an answer.
Anyone have a different approach?

 

[judas_priest]

My reading of the OP is that symmetry is the ordained method to be used.

Could you elaborate?

 

[judas_priest]

Oh, man. This was a simple problem. Turns out I was entering the answer right with the wrong syntax. It's an online quiz I'm taking. D/2 is the answer. I was putting parentheses around, and hence getting it wrong.