makepeace
- 2
- 0
Hello you clever people,
I'm having a bit of a logical problem with the deflection of a simple uniform cantilever beam loaded with a downward force on the free end.
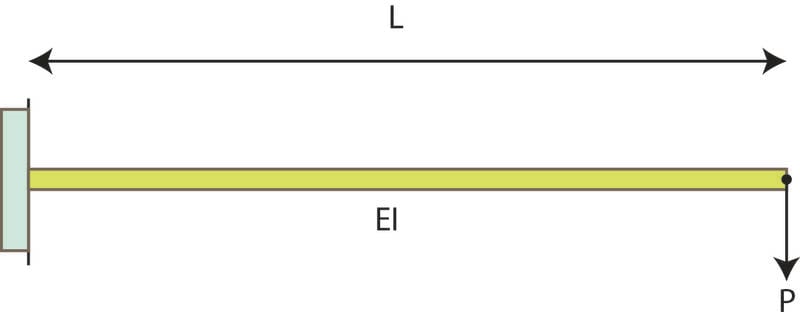
My intuition is that the beam would do something like this:

But most literature, and my mechanics of solids course at uni says this happens:
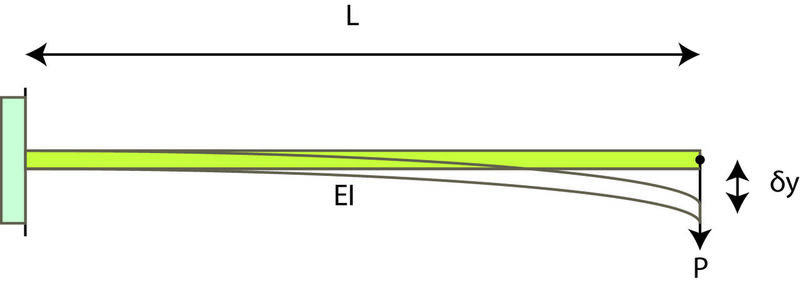
We're using Castigliano's theorem and so far we get that δy=PL3/3EI , but I'm convinced that there should be a horizontal component to the deflection.
If so,
Firstly: Is this horizontal deflection factored into the above derivation and if so how would one calculate the horizontal deflection? Could you just use the parameterization of the parabolic nature of the deflection?
or I guess you could work it out for from the slope?
Secondly: If the horizontal deflection isn't factored in, how would you derive it? I would imagine that the elastic strain due to the vertical deflection would have an effect on the horizontal deflection and vice versa until you reach your equilibrium point for the structure.
I hope that I'm just being silly and WAY overthinking this, please excuse if this is a trivial/stupid question.
P.S. please excuse my horrid drawings, and their size - couldn't figure out how to change that.
I'm having a bit of a logical problem with the deflection of a simple uniform cantilever beam loaded with a downward force on the free end.
My intuition is that the beam would do something like this:
But most literature, and my mechanics of solids course at uni says this happens:
We're using Castigliano's theorem and so far we get that δy=PL3/3EI , but I'm convinced that there should be a horizontal component to the deflection.
If so,
Firstly: Is this horizontal deflection factored into the above derivation and if so how would one calculate the horizontal deflection? Could you just use the parameterization of the parabolic nature of the deflection?
or I guess you could work it out for from the slope?
Secondly: If the horizontal deflection isn't factored in, how would you derive it? I would imagine that the elastic strain due to the vertical deflection would have an effect on the horizontal deflection and vice versa until you reach your equilibrium point for the structure.
I hope that I'm just being silly and WAY overthinking this, please excuse if this is a trivial/stupid question.
P.S. please excuse my horrid drawings, and their size - couldn't figure out how to change that.
Last edited: