lord_blurg
- 10
- 0
Hi, I missed two weeks of physics at school due to illness and I am having a hard time understanding a lot of the things our teacher set us to do. So I have these questions...
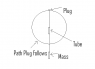
1. If an object is spinning in centripetal motion (View the dodgy diagram I made)
View Image 'Diagram.png'
If I were to change the radius of the string would the period (The time it takes for one complete revolution) change assuming the masses are kept constant? If the radius is changed will the force change on the plug? Will the speed of the plug change?
2. If the radius does not effect the period in any way, does that mean the radius is directly proportional to the period and thus r = T. (The equal sign is meant to be a proportional sign but I don't know how to do them with these forums)
3. If I were to draw a graph of r against T^2 would the graph appear linear or curved. What would the slope represent? Would it represent the acceleration, speed, or force.
4. View Image 'formula.png'
If I wanted to prove this, all I would do is get one of the formulas and substitute in all the variables which are in the formula I am trying to get proven right? Therefore I would have something which looks like this...
a=(2(pi)r/T)^2/r
And then I would have to manipulate that into the formula I am trying to prove... How in the heck would I do that lol.
I have done everything here but am trying to back up my answers. The only one I haven't done is number 4 and a just wondering if I am on the right track. The other questions I think I have gotten right but I am not completely basing my answers on fact but on the knowledge I have gotten from my teacher. I don't want to hand up a practical and be completely wrong =/
1. If an object is spinning in centripetal motion (View the dodgy diagram I made)
View Image 'Diagram.png'
If I were to change the radius of the string would the period (The time it takes for one complete revolution) change assuming the masses are kept constant? If the radius is changed will the force change on the plug? Will the speed of the plug change?
2. If the radius does not effect the period in any way, does that mean the radius is directly proportional to the period and thus r = T. (The equal sign is meant to be a proportional sign but I don't know how to do them with these forums)
3. If I were to draw a graph of r against T^2 would the graph appear linear or curved. What would the slope represent? Would it represent the acceleration, speed, or force.
4. View Image 'formula.png'
If I wanted to prove this, all I would do is get one of the formulas and substitute in all the variables which are in the formula I am trying to get proven right? Therefore I would have something which looks like this...
a=(2(pi)r/T)^2/r
And then I would have to manipulate that into the formula I am trying to prove... How in the heck would I do that lol.
I have done everything here but am trying to back up my answers. The only one I haven't done is number 4 and a just wondering if I am on the right track. The other questions I think I have gotten right but I am not completely basing my answers on fact but on the knowledge I have gotten from my teacher. I don't want to hand up a practical and be completely wrong =/
Attachments
Last edited: