superdave
- 149
- 3
An amusement park ride consists of airplane-shaped cars attached to steel rods. Each rod has a length of 14.5 m and a cross-sectional area of 8.25 {\rm cm}^{2}.
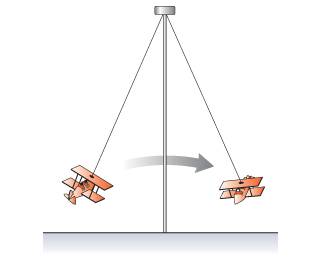
When operating, the ride has a maximum angular speed of 8.50 rev/min. How much is the rod stretched then?
Take the Young's modulus for the rod to be Y = 2.00×1011 Pa and the free fall acceleration to be g = 9.80 m/s^2
Assume that each car plus two people seated in it has a total weight of 1930 N.
Now, I somehow need to find theta or r using only omega. I'm not really sure how to do this.
When operating, the ride has a maximum angular speed of 8.50 rev/min. How much is the rod stretched then?
Take the Young's modulus for the rod to be Y = 2.00×1011 Pa and the free fall acceleration to be g = 9.80 m/s^2
Assume that each car plus two people seated in it has a total weight of 1930 N.
Now, I somehow need to find theta or r using only omega. I'm not really sure how to do this.