- #1
yhyoon0511
- 1
- 3
- Homework Statement
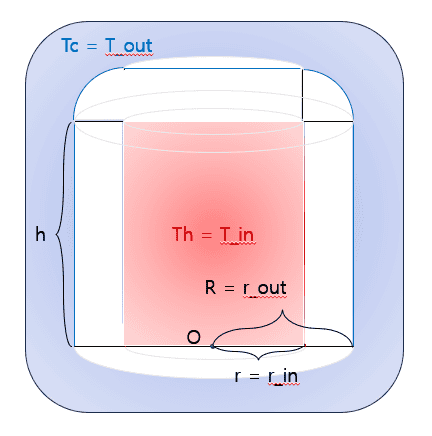
- What needs to be obtained is the temperature distribution of thermos that have reached thermal equilibrium. The thermos consists of three parts. The 'pillar' is a hollow cylinder whose inner radius is R_in and outside radius is R_out, height h. The 'lid border' is a solid of revolution made by rotating a quadrant with a radius of R_out - R_in. The 'lid center' is a cylinder, the radius and the height is R_out - R_in. The 'lid border' is placed on the 'pillar', and 'lid center' occupies the inside of the 'lid center'. The surface of the thermos is in contact with two heat sources. First, the high heat source which has a temperature of Th covers the inside. Next, the low heat source which has a temperature or Tl covers the outside except the bottom of the thermos. And the bottom of the 'pillar' is insulated.
- Relevant Equations
- Heat transfer equation
Lapace equation in cylindrical coordinate
This problem is created by my cousin who is learning about 1-D heat transfer problems. He made this problem and made solve it with fourier's law of heat transfer with calculating thermal resistance by integrating 1/A dx, which presupposes a false assumption; if the distance away from the heat source is the same, the temperature will be the same. I find out it was a wrong solution, but I can't solve this problem with my knowledge. The hardest problem I've solved used the separation of variables which assuming the steady state temperature can be expressed as R(r)Z(z)(applying this solution for this problem, theta term is omitted because there is theta directional symmetry). However, with r direction boundary conditions varying through the z direction, I don't think I can get suitable answer with this problem.