How Can I Improve My Algebra Skills for Solving Equilibrium Problems?

[posto002]

Homework Statement

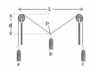
I'm supposed to find the vertical displacement of the hanging object in the middle by coming up with a formula for it. I am confused by this and was wondering if someone could help me out. I have a system with 2 pulleys and 3 weights. They are all held together by one string. There are two weights on the outside of the two pulleys, both have the same mass, which hold up the weight in the center.
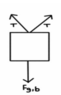
The system has a central object B with mass (M) which is suspended half way between two pulleys by a string. The whole system is in equilibrium. The objects
A and C, which are on the outside of the pulleys, have the same mass of (m).
What I need to solve for is: what is an equation for the vertical displacement of the central object B in terms of the horizontal distance between the two pulleys (L), the mass of object B (M), and the mass (m) of objects A and C?

Relevant Equations

none given

I got the equation --> d=mL/[2*(√(2M)^2-m^2)] where M is one of the masses at either end (multiplied by 2 because... there's two of them.) and m is the mass in the middle of the system. Something that a TA told me was that L, the horizontal distance of the system changes. I'm confused by this because during the lab, we never shifted the pulleys in anyway, nor were we required to. Can anyone explain this to me?

Any help is appreciated. Thanks.

 

[DEvens]

When I was in 4th year undergrad, one of my co-students taught me a very valuable lesson. The entire class, except him, were having a terrible time solving the homework problem. He was done. We asked him, how did you apply the hint the prof gave us? His response? "I never pay too much attention to what the prof tells us." He had gone to the library and read in a text how to solve the problem, and had done it that way. In a half hour. We were all struggling after three days of constant work.

The hint from the TA, the way you have described it, seems hopeless. Ignore it. The picture shows the middle pulley can move up and down. Presumably it will stay in the middle. (Can you give an argument that it will stay in the middle?)

Can you do a free body diagram for the mass in the middle? What is the condition that the system is at equilibrium? What must the tension in the string on each side be for that condition to be met?

For what angle $\theta$ is $\sin(\theta) = 0.5$?

 

[posto002]

When I was in 4th year undergrad, one of my co-students taught me a very valuable lesson. The entire class, except him, were having a terrible time solving the homework problem. He was done. We asked him, how did you apply the hint the prof gave us? His response? "I never pay too much attention to what the prof tells us." He had gone to the library and read in a text how to solve the problem, and had done it that way. In a half hour. We were all struggling after three days of constant work.

The hint from the TA, the way you have described it, seems hopeless. Ignore it. The picture shows the middle pulley can move up and down. Presumably it will stay in the middle. (Can you give an argument that it will stay in the middle?)

Can you do a free body diagram for the mass in the middle? What is the condition that the system is at equilibrium? What must the tension in the string on each side be for that condition to be met?

For what angle $\theta$ is $\sin(\theta) = 0.5$?

This is the force diagram for the middle object. In order for it to be in equilibrium, it should be set in the middle, as stated that it was, between the two pulleys. The two masses at the ends should be the same height from the ground. Because both end masses are the same, that would mean the tension on the string for both ends are the same and this equal to the two tensile forces acting on the string from where the middle object is hanging. Because the two masses at the ends are the same, they should accelerate upwards at the same rate that the middle object accelerates downward, so both tensile forces coming from either side of the middle block cancels out meaning it won't be moved to either side, but instead it will be pulled down because of gravity. In that case, it would stay in the middle. Am I correct?

As for the the angle Θ, wouldn't that be 30 degrees?

 

[haruspex]

I got the equation --> d=mL/[2*(√(2M)^2-m^2)] where M is one of the masses at either end

Looks right, except that you have swapped over the meanings of m and M.

Because both end masses are the same, that would mean the tension on the string for both ends are the same

The tension is the same throughout the string because it is considered massless and the pulleys frictionless. It is not affected by whether the masses are the same.

 

[DEvens]

Equilibrium means that the net force on the middle block is zero.

30 degrees is for the special case when the middle block has equal mass to each of the outer blocks.

 

[haruspex]

Equilibrium means that the net force on the middle block is zero.

30 degrees is for the special case when the middle block has equal mass to each of the outer blocks.

Seems to me the OP solved the question correctly (except for mixing up the two mass definitions) in post #1. The only issue was the TA's misleading advice, which you addressed in post #2.

 

[posto002]

Seems to me the OP solved the question correctly (except for mixing up the two mass definitions) in post #1. The only issue was the TA's misleading advice, which you addressed in post #2.

Thank you, haruspex and DEvens for your help. I appreciate it. Do any of you have any tips on completing physics exams faster? I have great grades on my assignments, but that's mainly because we have a whole week to complete them. I take about 3 days to complete around 15-20 problems, but when it comes to exams I flunk them terribly. I can't see how to come up with the answers fast enough and to have all the problems and formulas written down when there are billions and billions of different scenarios of physics problems that have to do with just one subtopic in physics. It's difficult to see the connections and figure out different variables I need all within the time I have to complete the exams.

Thanks, again, you two for helping me with this problem.

 

[haruspex]

Thank you, haruspex and DEvens for your help. I appreciate it. Do any of you have any tips on completing physics exams faster? I have great grades on my assignments, but that's mainly because we have a whole week to complete them. I take about 3 days to complete around 15-20 problems, but when it comes to exams I flunk them terribly. I can't see how to come up with the answers fast enough and to have all the problems and formulas written down when there are billions and billions of different scenarios of physics problems that have to do with just one subtopic in physics. It's difficult to see the connections and figure out different variables I need all within the time I have to complete the exams.

Thanks, again, you two for helping me with this problem.

I have lots of tips on checking algebra, but that takes more time, not less.
Maybe you are not using the most direct methods. Try posting some you have solved, but taking a while, showing all your working.

 

[posto002]

I have lots of tips on checking algebra, but that takes more time, not less.
Maybe you are not using the most direct methods. Try posting some you have solved, but taking a while, showing all your working.

Sorry that my reply is taking awhile. I just got another assignment that I wish to get done before as soon as possible. I'll try to get an example as quick as I can after I've completed the assignment. I am interested in learning any new tips from you, and I thank you for your help.