themagiciant95 said:
Nice. But, if the potential difference in the wire in very small compared to the one of the resistor, then the current cannot be the same in every part of the circuit.
Choose two points on the wire and the potential difference between those points is very small. The current ##I## that flows through that piece of wire equals ##\frac{V}{R}## where ##V## is that potential difference and ##R## is the resistance of that piece of wire.
Now choose two points, one on each side of the resistor and the potential difference between those points is much larger. The current ##I## that flows through that resistor equals ##\frac{V}{R}## where ##V## is that potential difference and ##R## is the resistance of that resistor.
The resistance of the resistor is much larger than the resistance of that piece of wire, the potential difference across the resistor is much larger than the potential difference across the resistor, but the current through them is the same.
It's better to not speak of the potential "in" a wire. You can have a potential
at a point in the wire, and thus a potential difference between two points along a wire. It is okay, though, to speak of current in a wire. The reason is because the current is the same at every point along a wire, but the potential is not (assuming a current flows through the wire).
By the way, Ohm's Law is not the assertion that the current equals ##\frac{V}{R}##. Rather, it's the assertion that as you change the potential difference ##V## between two points the current changes in proportion, in other words, the value of ##R## remains the same. Such a thing never actually happens, but in many cases it's a good approximation. In others, though, such as an incandescent light bulb, it's not.
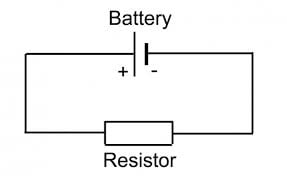 I know that if a consider the wire from the + of the battery until the + extreme of the resistor, in this portion the wire has the same potential. The same thing regarding the portion of the wire beetween the - of the battery until the - of the resistor.
I know that if a consider the wire from the + of the battery until the + extreme of the resistor, in this portion the wire has the same potential. The same thing regarding the portion of the wire beetween the - of the battery until the - of the resistor.