How Do Equilibrium Conditions Relate to Forces in a Bridge Member?

[student45]

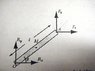
If there is a cross member of a bridge with two forces (F and R) acting as contacts at the ends of the member, is there a way to use equilibrium conditions to write the relationships between the forces? The member makes an angle theta with the horizontal (upward and to the right) and has a center of mass at its geometrical center, with the origion (O) chosen at the point where R is acting (on the left end of the member). I'm just not sure how to approach this. All I know is that net force and net torque are both equal to zero, but I have no idea where to go from here. Thanks.

 

[ponjavic]

drawing a FBD would help us interpret the problem

 

[Zipp425]

I Have the same problem

Hey, I know that this post is from a while ago, but I have the same problem...

Attached is an FBD of the problem.

 

[PhanthomJay]

Hey, I know that this post is from a while ago, but I have the same problem...

Attached is an FBD of the problem.

If you ignore the weight of the member, the equilibrium conditions must be satisfied (Fy and Ry are equal and opposite, Fx and Rx are equal and opposite, and further, since the member is a 2-force member (axial loading only), then Fy/Fx = Ry/Rx = tan theta.

If the weight of the member, acting thru its c.m., is considered, it is often customary to split its weight half and half, and apply that value to the adjacent joints. You still get the same relationships of the forces.

If the weight of the member is significant and must be considered as it actually acts thru its c.m., you still get the same equilibrium relationships between F and R, but you no longer have the Fy/Fx = tan theta relationship, because you no longer have a pure truss, you have a frame with shear loads introduced as well as axial loads.