mikel lowery
- 2
- 0
Hi, I am really stuck here. My problem is with determining the support reactions. I understand that this needs to be done first before working on each truss member. But I don't understand how to determine them. I have read and re-read all my available text and still stuck.
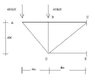
The question I can't solve, " Determine the force in each member" of the attached. Each joint are pin joints.
Can some one please walk me through this?
Regards
Mikel
<- Edit ->
I have tried to solve rather than just ask, I'm aware that the 3 laws of equilibrium apply for the reactions, sum of x =0, sum of y= 0 and sum of Mc = 0. I just don't understand 1. Where the reactions are and 2. how to determine them?
The question I can't solve, " Determine the force in each member" of the attached. Each joint are pin joints.
Can some one please walk me through this?
Regards
Mikel
<- Edit ->
I have tried to solve rather than just ask, I'm aware that the 3 laws of equilibrium apply for the reactions, sum of x =0, sum of y= 0 and sum of Mc = 0. I just don't understand 1. Where the reactions are and 2. how to determine them?
Attachments
Last edited: