How do I determine the wretched coefficient of kinetic friction? It's impossible

[riseofphoenix]

A 3.40 kg block is pushed along the ceiling with a constant applied force of 85.0 N that acts at an angle of 55.0° with the horizontal, as in the figure below. The block accelerates to the right at 6.00 m/s². Determine the coefficient of kinetic friction between block and ceiling.

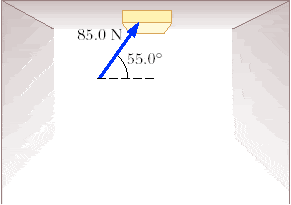
Ugghhh so... this is what I did...

F = 85.0 N
m = 3.40 kg
a = 6.00 m/s²
f_k = μ_kn

1) Forces in the x-direction:
F cos θ
f_k (kinetic friction)

Forces in the y-direction:
F sin θ
n (normal force)

2) Sum of forces

ƩF_x = F cos θ + f_k = 0
ƩF_y = F sin θ + n = 0
ƩF_y = F sin θ + n = 0
ƩF_y = n = -F sin θ

3) ƩF_x = F cos θ + μ_kn = 0
3) ƩF_x = F cos θ + μ_k(-F sin θ) = 0
3) ƩF_x = F cos θ + μ_k(-F sin θ) = 0
3) ƩF_x = 85 cos 55 - μ_k(85 sin 55) = 0
3) ƩF_x = 85 cos 55 = μ_k(85 sin 55)
3) ƩF_x = (85 cos 55)/(85 sin 55) = μ_k
3) ƩF_x = 0.700 = μ_k

So I got this wrong, the answer is actually 0.781 (?)

I don't know what to do!

 

[riseofphoenix]

And THEN, i tried doing this:

ƩFx = F cos θ + μ_kn = 6

85 cos 55 + μ_k(-85 sin 55) = 6
85 cos 55 - μ_k(85 sin 55) = 6
85 cos 55 = 6 + μ_k(85 sin 55)
48.75 - 6 = 69.62μ_k
42.75/69.62 = μ_k
0.614 = μ_k

-____-

I didn't get that answer!
Can you please show me how to get to that answer please?

 

[gneill]

I don't see where you've taken gravity into account. Won't it affect the normal force?