How Do Levers Work? Explained Simply

[pete]

So my last drawing was too confusing so I’ve tried to sketch it as simply as possible to explain. In the first picture a lever in red is prying the two blue parts apart. The Blue parts are fixed.
I’m not too good at all this but as I understand it the arm of the lever is twice as long on the side with the force being applied so the force is doubled, then equal applied to both half's of the blue part.
Given that I’ve understood that correctly then in the second picture the same is happening except that the lever instead of acting on the inside of the blue part is acting on another lever. The first lever is 3 to 1 so that’s 1.5 pushing on the pivot and 1.5 on the next lever and so on.
What I’m asking is do levers work in sequence like this or do you calculate it somehow as one long lever? Or is it all completely wrong?

 

[timthereaper]

The best way to learn how these levers work is by drawing the free-body diagrams yourself and labeling the forces. Presumably you want to analyze these statically, so when determining the forces it's helpful to keep in mind that the sum of the forces in any component direction must be zero. Making other assumptions such as perfectly rigid bodies and prismatic beams is helpful as well to see the underlying physics of the problem.

 

[pete]

I'll give it a go. Any comment on whether I'm doing it right in the picture above?

 

[pete]

I watched a few tutorials on free body diagrams and they look very helpful but I do not really understand how to use them in the case of levers and I don't see how they are any use to understand the maths behind them.
For a lever its the mass x the distance to the fulcrum x the distance to find the force applied. What I don't understand is if you have a lever acting on another lever or a set of levers in sequence do you calculate each lever individually as I did in the picture above or is that wrong, am I doing it wrong?
If I draw free body diagrams without understanding the underlying maths how will I know how long my arrows should be?
Or have I misunderstood you, are you asking me to draw a free body diagram because you don't understand the picture I’ve done? I’ll give it a go but it’s going to look very similar I think.

 

[pete]

I tried to draw the problem and my solution out clearer here:

 

[Mark44]

For a lever its the mass x the distance to the fulcrum x the distance to find the force applied.

No, it's the force times the distance to the fulcrum.

What I don't understand is if you have a lever acting on another lever or a set of levers in sequence do you calculate each lever individually as I did in the picture above or is that wrong, am I doing it wrong?

Your pictures in post #5 are confusing, since it's unclear whether either of the two bodies shown is fixed. The idea with a lever is that the fulcrum is fixed, but each arm of the lever is allowed to move. In your drawing is the L-shaped body allowed to move? Is the small rectangle allowed to move?

The basic idea of a lever is that the two moments are equal. Looking at the right-most lever in your drawing in post #5, let's assume for now that its fulcrum is fixed. If a force F is applied to the right end, at a distance of 3m from the fulcrum, the moment is 3 x F (probably in units of Newton-meters). The moment at the left end of this lever is also 3 x F, but since the lever arm is only 1 m., the force is 3F. Again, assuming the fulcrum is fixed, the only forces to consider are the forces at each end of the lever, not the force down on the fulcrum itself.

Both of your levers have forces applied at the ends of the levers, but levers also work with with fulcrum being at one end. For example, when you use a crowbar to pull a nail out of a piece of wood, you apply a relatively small force at the end of the crowbar (with a long lever arm), and the crowbar applies a much greater force with a shorter lever arm to the nail. For example, if the crowbar is 1 ft long, with the fulcrum at the far end of the crowbar, and you apply an upward force of 50 lb, the moment of your applied force is 50 ft-lb. If the force on the nail is applied 2" from the end of the crowbar, the moment is also 50 ft-lb, but the pulling force is 300 lb.

Your moment: 50 lb x 1 ft = 50 ft-lb
Nail moment: 300 lb x 1/6 ft = 50 ft-lb

 

[pete]

Thanks for helping me out with this. I remember from school that the force (not the mass) is multiplied by the distance from the fulcrum. This is clear, if F is 100N then it will apply 200Nm upwards on Body A.

What I’m trying to understand firstly is if A and B are fixed and with F you are trying to force them apart how do you calculate the force on the two body's?

 

[Mark44]

Thanks for helping me out with this. I remember from school that the force (not the mass) is multiplied by the distance from the fulcrum. This is clear, if F is 100N then it will apply 200Nm upwards on Body A.

What I’m trying to understand firstly is if A and B are fixed and with F you are trying to force them apart how do you calculate the force on the two body's?

View attachment 220549

If A and B are fixed, you can't pry them apart. "Fixed" means that they don't move. If the fulcrum (fixed point) is at A, and you apply a downward force of 100 Nt at the end, there will be a force of 200 Nt downward at B.
Similarly if the fulcrum is at B, a 100 Nt downward force at the end results in a 200 Nt force upward at A.

 

[Mark44]

I remember from school that the force (not the mass) is multiplied by the distance from the fulcrum.

The defining equation says that the two moments will be equal.
If F_A is one of the forces, applied at a distance of L_A from the fulcrum, the moment is F_AL_A. The other moment, defined similarly, is F_BL_B. The equation is F_AL_A = F_BL_B.

 

[pete]

If A and B are fixed, you can't pry them apart. "Fixed" means that they don't move. If the fulcrum (fixed point) is at A, and you apply a downward force of 100 Nt at the end, there will be a force of 200 Nt downward at B.
Similarly if the fulcrum is at B, a 100 Nt downward force at the end results in a 200 Nt force upward at A.

A few people have said this to me that it’s fixed or it’s not and you can't talk about force on a fixed object. This question is from looking at a type of clamp and it can be very tightly done up or very loose without the two clamping surfaces moving about. What the object was fixed but had a breaking point of 500Nt, there must be a way to talk about the forces acting on a fixed object to understand when it’ll break?

 

[pete]

So for example if A and B are fixed unbreakable scales, so that when I push down on the lever I see the scales at A and B both move up. Now as in your example you apply 100Nt downward force at the end, what will the scales read? Will they both read 200Nm? Do they read the same? How do I work this out? What I’ve been doing in my attempt at a solution to the two lever problem was divide it in half, so 100Nt on A and 100Nt on B but I don't know if I’m doing it right?

 

[CWatters]

What I’m trying to understand firstly is if A and B are fixed and with F you are trying to force them apart how do you calculate the force on the two body's?

Lets put some directions on the forces...

Lets say F = 10N.

If the lever isn't accelerating in rotation then the net torque must be zero. If we define clockwise as positive then taking moments about point B we can write..
-(A*1) + (2*F) = 0
or rearrange that to give..
A = 2F
and so A = 20N

If the lever isn't accelerating vertically then the net vertical force must also be zero. If we define up as positive then we can write..

(-A) + (+B) + (-F) = 0
or rearrange to give
B = F + A
= 10 + 20
= 30N

 

[pete]

Those arrows really helped, Thanks, I appreciate the help. I've not disappeared I'm just trying to solve my original picture with the two levers in sequence.

 

[pete]

What I am confused about is that the clamp or anything you try to pry something apart with always applys equal pressure to both sides. If I push a lever, a crowbar between two posts and apply pressure it dose so to both sides equally, I thought? But in the examples like the one above you showed A and B are different? A=20N B=30N.
So in this picture: If A and B are the two surfaces and the lever a crowbar it should apply equal force to A and B. Whats the difference between my problem here and the example you gave?

 

[pete]

So if F is 10Nt then A and B must both be 20Nt? I think the confusing thing is the idea of a kind of balance or see-saw with weights on ether side when I'm looking at a clamp between two surfaces. There is no up or down.

 

[Mark44]

What I am confused about is that the clamp or anything you try to pry something apart with always applys equal pressure to both sides. If I push a lever, a crowbar between two posts and apply pressure it dose so to both sides equally, I thought?

Yes, because both surfaces you're trying pry apart have the same lever arm.
In your drawing the two posts don't have the same lever arms. If A is the fulcrum, a 10 N force downward at the right end causes a 30 N force downward at B. If B is the fulcrum, the same 10 N force downward at the end causes a 20 N force upward at A.

 

[pete]

So if A and B are round steel posts seen from above and the black line is a bar and I pull at F which is the fulcrum? I don't understand how there can be two answer to the problem. The only variable in the drawing is how much force you apply to the lever is it not?

 

[pete]

OK I think I understand. By fulcrum you mean one is fixed, say A and then the lever turns around it against B or B is fixed and the lever turns around it against A. But this is back to the same problem. They are both fixed. Like the clamp applying pressure to the inside of the fitting. They are both the fulcrum. Again if A and B were unmovable unbreakable scales giving a reading and I applied 10Nt to the end of the lever then what reading should I get at A and B? 20Nt?

 

[Mark44]

So if A and B are round steel posts seen from above and the black line is a bar and I pull at F which is the fulcrum? I don't understand how there can be two answer to the problem. The only variable in the drawing is how much force you apply to the lever is it not?

Here's my understanding, which others are free to refute (it's been many years since I took a physics class);
Since the force against B will be 50% greater than the force against A, the post at B will be the one that is most likely to give. That's assuming that both posts resist with the same force.

Do you understand where I got the 50% figure? If not, around post B, the force applied to A is twice the force F, because one lever arm is 2 m. and the shorter lever arm is 1 m. Around post A, the force applied to B is three times the force F, because one lever is 3 m. and the shorter lever arm is 1 m.

 

[pete]

So if I take the scales example the reading I will get at A will be 20Nt, this is clear, but the reading at B your saying will be 30Nt. That derived from the length of the lever times the distance between A and B? I must be confused because that dose not seem to make sense, the force at B would increase the closer B got to your hands which is the wrong way round. How did you get the 30Nt at B?

 

[pete]

I found it, it's a second class lever. So the force times the length of the lever = 20Nm, that's the "moment?" on one side to find the other it's 20Nm divided by distance from A to B. So 20Nm. They are equal but only by coincidence. Anyhow I've had another go at the problem with my new physics powers, what do you think? I put the scales into try and help with the confusion.

 

[Mark44]

My response before related to your drawing in post #14.

So if I take the scales example the reading I will get at A will be 20Nt, this is clear, but the reading at B your saying will be 30Nt. That derived from the length of the lever times the distance between A and B?

No.I explained my reasoning in post #19.
Assuming that we consider A as the fulcrum, we have two moments. One is F x 3, or 3F. The other is ? x 1. For these moments to be equal, 3F has to be equal to ? x 1, so the force acting at B is 3F, or three times the force that is applied.

I must be confused because that dose not seem to make sense, the force at B would increase the closer B got to your hands which is the wrong way round. How did you get the 30Nt at B?

Why would B get closer to your hands. I'm not assuming that points A and B are moving laterally.

 

[pete]

No their not moving I just got it wrong, I see what you mean now I'll have another go at it.

 

[Stephen Tashi]

I must be confused because that dose not seem to make sense, the force at B would increase the closer B got to your hands which is the wrong way round.

If you imagine the goal is to exert a 10 Newton force on A, then the closer B is to your hands (where force F is applied) the more force you would have to exert there to accomplish that goal. So it makes sense that the force on B would increase.

You are imagining a situation where you have picked a force to exert with your hands and you are willing to let the forces on A and B take whatever values are needed to balance the situation. In that situation, it is true that the closer B is to your hands, the less force is exerted on A (and thus on B).

 

[CWatters]

You can see the diagram in #21 must be wrong by looking at the external forces...you have 90+10=100N acting downwards and only 60N upwards so there is a net force of 40N downwards. It implies the whole assembly is accelerating downwards.

 

[CWatters]

You can see the diagram in #21 must be wrong by looking at the external forces...you have 90+10=100N acting downwards and only 60N upwards so there is a net force of 40N downwards. It implies the whole assembly is accelerating downwards.

Correction: I made a mistake with the directions, that should be 60+10=70N downwards and 90N upwards. Still doesn't sum to zero so it's accelerating.

 

[pete]

I don’t understand the accelerating downward bit, it’s a clamp restricted between two scales it can't go anywhere and I don’t see why it has to be balanced. If I had a fitting with a bolt that you tightened so it came out of one side then all of the force would come from that point but as it did so it would push it’s self against the opposite side so the force would be equal on both sides, in a 2D representation. Though different amounts of force are applied on both sides I then add them together and divide it by 2 to give the results on the scales. Here’s another go at:

dose this one look right?

 

[pete]

Or do you mean both side have to add up to the same no matter what?

 

[Mark44]

Though different amounts of force are applied on both sides I then add them together and divide it by 2 to give the results on the scales.

Which is not how it works. In this drawing, there's a force of 90 N on the upper scale, and a force of 100 N on the lower scale. If the upper scale reads 80 N, then that's the upward force, and similarly for the lower scale.

 

[Mark44]

Or do you mean both side have to add up to the same no matter what?

If the system has a net force in some direction, then it will accelerate in that direction -- F = ma is the basic equation here.

 

[pete]

When you say it will accelerate in a direction what do you mean? Do you mean it will actually fly off somewhere or is it some kind of rule that your referring too? When you looked at the drawing in post #14 you pointed out that there was a 30N force on the body B and a 20N force on the body A but did not talk about it accelerating anywhere. If the crowbar can apply more force to one post that the other why can the clamp not do it?
If I stand between two walls and push against one wall with my back against the other I’m applying all my force in one direction but I feel it equally on my back. If I put a scale behind me and one in front of my hands they would read the same despite me pushing all my force in one direction. This is why I took the total force, unbalance, 90Nt to the right and 100Nt to the left combined them then dived them by 2 to give the readings on the scales, what is it I am doing wrong?u say it will acc

 

[Mark44]

If I stand between two walls and push against one wall with my back against the other I’m applying all my force in one direction but I feel it equally on my back.

Yes, because your arms are applying a force against one wall and your back is applying an oppositely directed force to the other wall. The magnitudes of the forces are equal, but their directions are opposite. Note also, that each wall is also applying a force against you. If you can apply a greater force than either wall can match, there will be motion of one or both walls.

If I put a scale behind me and one in front of my hands they would read the same despite me pushing all my force in one direction.

You're actually pushing in two directions. Even if there weren't a wall behind you, to push against the wall with your arms, you have to push against something with your feet (the ground). If you were on slippery ice, you wouldn't be able to push against the wall.

 

[pete]

OK I understand this and it seems to make sense to me that both should be equal. To do the calculations though I have followed the rules we have been talking about and this drawing is just a more complex example of the drawing in post #14. This is why I drew #14 and tried to solve it first to understand the rules so if it unbalanced in #14 it’s going to be unbalanced in this one. What am I missing?
Here is the shape between the two walls and the lever and seems no matter how I do it it will always be more force on one than the other?

 

[CWatters]

That is correct, there will be more force on the lower "wall". The force on the lower wall will be equal to the sum of the force on the upper wall and the applied force.

Consider the lever on its own. Newton's law F=ma applies. If a =0 then the net force f=0. In other words the vertical forces sum to zero as I explained earlier.

 

[CWatters]

Your drawing in #27 looks correct.

 

[pete]

I don’t really understand some of the terminology you use, the sum of the force on the upper wall, that’s the numbers I get from doing the first class lever calculation? And the applied force, that’s the number I get from doing the second class lever calculation I guess?
And everything summing to zero. The walls will always be stronger than the clamp so won't the force always sum to zero? I don’t know how to apply an equation with acceleration to a static object. You talk about acceleration a lot and I really don’t understand what you mean when everything if fixed in place.
It’s good that the drawing looks OK, was it not a problem that the numbers for the two walls are different, I though they had to be equal? That’s the summing to zero bit?

 

[Tom.G]

Consider this.

1. We consider the bottom wall to be fixed (such as attached to the floor)
2. There is some upward force being supplied (via the lever) to lift the upper wall
3. Consequentially, since the upper wall is immovable, there is an equal downward reaction force
4. This reaction force is supported by the lower wall (if you assume equilibrium)
5. To supply the lifting force to the upper wall, there is a (smaller) downward force at the right end of the lever
   (perhaps you standing there and pushing the lever down)
6. Again for equilibrium, this downward force at the right end of the lever must be supported by something (again, the lower wall), otherwise things are going to move

As you can probably see, the lower wall is supporting all the downward forces; which is the sum of the reaction force at the left of the lever plus your downward force at right of the lever. This holds whether the top wall is fixed, is a free weight that is not being lifted, or is attached to the bottom wall.

In general, for a fulcrum to be considered 'fixed' it must somehow be referenced to some applied force. In this scenario the reference is the floor you are standing on, and the fulcrum (the lower wall), being attached to it.

An alternate configuration could be the upper wall being a free weight and the lower wall being spring mounted to the floor. For this situation, you might want to consider the free weight at the left end to be the fulcrum (i.e. maintain its position), while you apply a force to the right end of the lever. Here the reference could be the Earth thru Gravitational coupling and eventually to the floor.

Well, this ended up a rather esoteric post. I hope it helps rather than confuses.

Cheers,
Tom

 

[CWatters]

I don’t really understand some of the terminology you use, the sum of the force on the upper wall, that’s the numbers I get from doing the first class lever calculation? And the applied force, that’s the number I get from doing the second class lever calculation I guess?

Imagine you had 1000+ levers all arranged in some complicated way between points A,B and F. Let's draw a box around those levels and call it a block. If the block is stationary then it's not accelerating so the external forces at A, B and F must sum to zero.

And everything summing to zero. The walls will always be stronger than the clamp so won't the force always sum to zero? I don’t know how to apply an equation with acceleration to a static object. You talk about acceleration a lot and I really don’t understand what you mean when everything if fixed in place.

It doesn't really matter _why_ it's stationary. If it is stationary it's not accelerating so the net force acting on it (in any direction) must be zero.

In this case we are assuming all your forces are vertical so we can write...

(-A) + (-F) + (+B) = 0

The signs in brackets are needed because this is vector addition and we need to take into account the direction of the forces acting on the block of levers.

It’s good that the drawing looks OK, was it not a problem that the numbers for the two walls are different, I though they had to be equal? That’s the summing to zero bit?

Indeed. Not only is the whole block of levers stationary (eg not accelerating) but each individual lever in the block is stationary (not accelerating) so the vertical forces on each individual lever will sum to zero. The force at points A can't be equal to B because of F.

Note I'm assuming that F acts vertically. If it acts at an angle then you have to use the vertical component of F in the sum above. The horizontal component of F would then cause there to be a horizontal component at A or B. This is because the horizontal forces must also sum to zero if the block of lever is stationary (eg not accelerating) horizontally. But perhaps best we assume F is vertical until you fully understand this.

 

[CWatters]

This issue of forces summing to zero is important... Consider an aircraft flying along straight and level at some constant speed.

It's not accelerating vertically so we can write...

Lift + (-weight) = 0

or rearrange that to...

Lift = weight

Likewise it's not accelerating horizontally so we can write...

Thrust + (-drag) = 0

or rearrange it to give

Thrust = drag

So even though the airplane is moving (but not accelerating) you can apply Newton's f=ma to the situation.

 

[pete]

I had to get some sleep, we are in different time zones.

I understand that an object must have equal forces operating on it or it will start moving in the direction of the weakest force proportional to the discrepancy, this makes sense to me. As with the aeroplane.

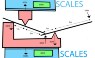
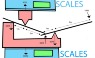
When you talk about the drawings I find the up down thing very confusing. All of these drawings are of me trying to refer to a clamp and are top down, looking down on the drawings from above. So everything is equal and talking about lifting things throws me off a bit.

I’m very pleased that the calculations I did are correct, you say the whole block of levers are stationary and nothing is accelerating and all the maths looks good to me as far as I understand the two equations I have to solve this.

But the total force one way is 90 and the other totals 100 so they are not equal. As the example of standing in an ally way pushing on the wall, if I apply pressure with my hands I also apply pressure with my back and it must be equal, a zero sum or I would accelerate towards one wall.

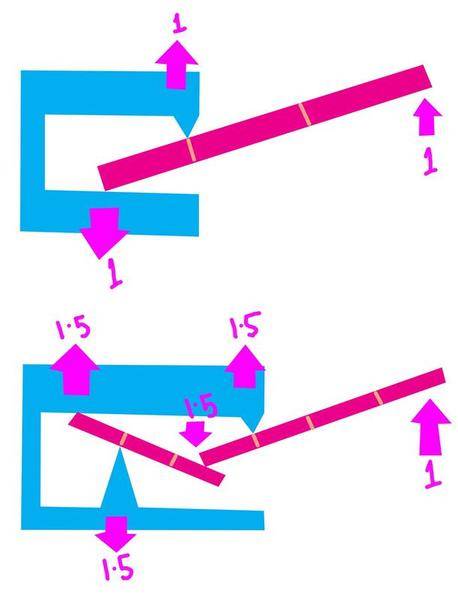
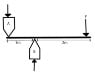
This leads me to exactly what I’m confused about. I think I understand the zero sum thing, if it’s not then it’s moving. That makes sense to me. So I’ll explain very specifically what’s not adding up for me. In this example. Let's say we are looking down on a gap in a wall. The wall is to heavy to move and to hard to break. I’m going to apply force on the lever and at 30n the surface of the lever will deform leaving marks and this is what I want. I want to apply enough force to do the job but no more.

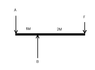
First I look at B, using A as the fulcrum. The difference in the distance of B to A and B to The force is 3 to 1! So I times the Force by 3, 30n at A. That’s my answer, 30n acting to the right on the wall at B and I get my mark on the lever.

Now A, I take the distance from the new fulcrum B to the Force, that’s 4, and times it by the force, that’s 40n, then I divide this by the distance from A to B to find the force at A and it’s 40n acting on the wall to the left at A. it’s 10 too much and I make a bad mark in my lever.

And this is where I’m confused. I’ve done the maths correctly as far as I can tell and the force to the right, 30n, is different to the force to the left 40n.

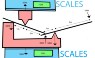
Lets look at the clamp, here it is from above in a crack in a wall. As the lever expands the clamp the two sides bite into the wall but as in the example of me pushing my hands against the wall the force to the right and the left will always be the same because as you said you are always pushing in two directions. This is an absolute, there will always be the same force on ether side of an expanding object between two fixed planes, I just can imagine being able to push more with my hands than my back!

So I don’t understand how to resolve this. In my solution with the 2 levers I added the total force together and divided it by 2. It’s the only thing I could think of to do to resolve the numbers.

So in this case I’d take the 30n on B and the 40n on A and add them together to get 70n, divide them in 2 to get 35n. Both A and B make a mark in the lever but nether make a hole. But I did this because the answer did not fit and I’m not sure if I can?

I noticed some other folk joined in while I was asleep, trying to explain this to me and I appreciate the help. I am getting there and I’m trying do my own research too to fill in the blanks but I just seem to be stuck on this point.

 

[CWatters]

First I look at B, using A as the fulcrum. The difference in the distance of B to A and B to The force is 3 to 1! So I times the Force by 3, 30n at A. That’s my answer, 30n acting to the right on the wall at B and I get my mark on the lever.

Now A, I take the distance from the new fulcrum B to the Force, that’s 4, and times it by the force, that’s 40n, then I divide this by the distance from A to B to find the force at A and it’s 40n acting on the wall to the left at A. it’s 10 too much and I make a bad mark in my lever.

And this is where I’m confused. I’ve done the maths correctly as far as I can tell and the force to the right, 30n, is different to the force to the left 40n.

It will be different. You have done the maths correctly, you just don't like what the maths is telling you :-)

The Applied force is 10N.
The force at B is 30N.
The force at A is 40N.

Here is the Free Body Diagram for your lever showing the forces on the lever...

You can see how the horizontal forces sum to zero which is exactly what you expect if the lever isn't accelerating.

Your drawing with the clamp should look more like this...

Now your "back" and "hands" are pushing with same force. Your "back" pushes with 40N (at A), one hand pushes with 30N (at B) and the other hand 10N (at F). Newton is happy, the force on both walls is the same.

Adding more levers doesn't change anything.

 

[CWatters]

Perhaps this achieves what you are trying to do? The force on both walls would be the same...

 

[pete]

That’s it! It’s a threaded bolt not a spring but I think this is what has been driving me mad. So If the bolt is screwed tight applying 20n force, that will be 10 in each direction and the whole thing will add up. Is this right?

If it was a lever that someone was pulling on, like a crow bar jammed in a gap then picture could be unbalanced, not add to 0, but only because we don’t see the whole system. If I drew the guy doing the pulling with his feet on the floor then I could balance the whole system?

 

[CWatters]

That’s it! It’s a threaded bolt not a spring but I think this is what has been driving me mad. So If the bolt is screwed tight applying 20n force, that will be 10 in each direction and the whole thing will add up. Is this right?

Yes but the screw would only need to apply 10N on the lever. The 10N it applies to the wall comes free due to Newton's third law.

 

[CWatters]

That’s it! It’s a threaded bolt not a spring but I think this is what has been driving me mad. So If the bolt is screwed tight applying 20n force, that will be 10 in each direction and the whole thing will add up. Is this right?

Yes but the screw would only need to apply 10N on the lever. The 10N it applies to the wall comes free due to Newton's third law.

 

[pete]

Yes I think I got you, I’m not too up on these laws but at a guess its the one about an equal and opposite force. The screw can only be tightened in one direction I just figured that if it pushed 10n onto the lever then it had to push back 10n too.
After 2 days of staring at this I think I’ll remember it too my grave. Thanks to everyone who posted trying to explain this to me especially Mark who really stuck in there when I couldn't get my head around it. It’s been a real help.

 

[Mark44]

especially Mark who really stuck in there when I couldn't get my head around it

You're welcome!