How do pressure gradients develop instantaneously in Bernoulli flow?

[Quentin_C]

Hi I am having trouble understanding how Bernoulli’s pressure gradients develop

I know the equation in a steady flow state (after the developed state ‘flushes’ thru) but I want to understand what mechanism lowers the pressure and increases the speed as the flow develops
The continuity principles tells us that this all must happen instantaneously

Here is my example
A funny shaped log is floating just submerged down a river flowing at 1 ms matching the current

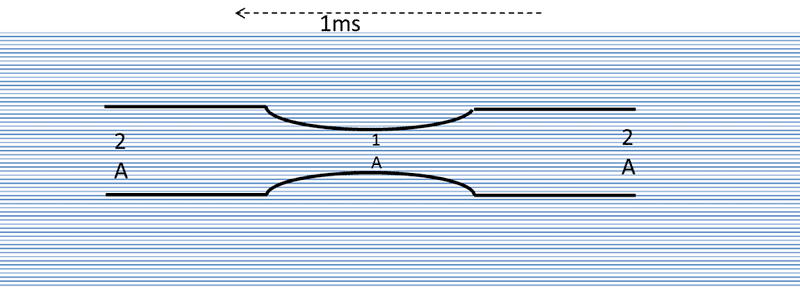
All of a sudden the rock very suddenly snags and stops it dead (with new velocity of 0ms) - the river continues to flow at 1ms
As I see it nothing has occurred to the internal fluid so this still travel at the same speed at equal pressure

But I know that it doesn’t but how?

Attempt at a Solution Conservation of Mass
For volume of water (1ms *2A) to enter the pipe - the corresponding amount of water has to exit the pipe (1ms *2A) therefore for our control volume to balance we must have 2ms*1A in the constriction –

Somehow the constriction has increased in speed

This means at that instant the fluid entering the pipe is traveling at 1ms and the fluid exiting the pipe is flowing at at 1ms but what mechanism that instant increases the speed in the constriction 1A and why ?

Work - the fluid in the constriction is experiencing no work it is being accelerated by the fluid entering the constriction as much as it is being decelerated by the fluid in front

Constant Energy Density
This must mean that’s the pressure at 1A must drop where as in the instant before this happens it is traveling at 1ms and the pressure is equal to the rest of the stream

Becomes

Somehow the pressure that has decreasedInstantaneously there is no reason for this to happen, as no work has occurred Deceleration in fron =Acceleration behindPressure gradient – in the instant before the fluid did not have a pressure gradient in front or behind it was all equal and equal to the free stream so it did not accelerate down a gradientHow do the Bernoulli conditions develop instantaneously as conservation tells us they should ?

 

[boneh3ad]

They don't develop instantaneously. Bernoulli's equation is not valid here because there is a transient period while the flow develops, and Bernoulli's equation is only valid in a steady flow.

 

[Quentin_C]

Is that really the case ?

The stream is going to provide flow at 1ms and take it at 1ms. Unless we are to somehow slow the whole of the flow in front or slow the flow of the stream behind .

If we can’t then under continuity the stream provides 1ms in at 2A and 1ms out at 2A, meaning that we have to have 2ms in the 1A constriction
It also doesn’t matter how small a time scale we work on the ratios are the same.

This leads me to conclude this must happen instantaneously.

It also lead me to conclude that the pressure difference in this situation is in some ways a result not the cause (as I have seen often stated) of the increase in speed. At best it is concurrent and independent.

Will the stream slow ?

If we consider a very long stream we are talking a large mass so to slow the flow above would be an amazing force

Equally without equal volume/ mass replacing it there would be a very large suction force as the stream continues under inertia away from the log constriction.

I am not sure that anything that occurs in this constriction will provide the work to slow the flow toward or the flow away.
However thinking about these inertial flows led me to a possible solution?

Attempt at Solution
It involves the inertial flow creating some acceleration in the stream entering and the inertial flow behind creating a suction force that allows static pressure to be converted to flow/dynamic pressure

1 ) Inertial Entry acceleration
As the volume per second at the entrance must continue there is a larger volume/mass entering than inside the construction

at T0

at T1 under inertia

Now this can’t happen but the larger entry mass/KE acts on the smaller and smaller mass contained causes work on the smaller volume/ mass in front thus accelerates it

This would cease when the throat speed (exit) is accelerated to 2v- the exit speed that fully dispenses the entry volume 2A at 1v.

The problem is that as this is action is purely inertial.
The Total KE is the same (just shared with a smaller and smaller mass in the constriction) So we haven't accounted for all of the KE increase to increase throat speed to the required velocity 2V to deal for the whole volume- We also require a conversion of static pressure to dynamic to balance the energy equation.

This is provided by

Inertial Exit Suction

Equally the volume just behind the exit will continue to flow (by inertia) away and must be replaced by the volume in the expansion - while this is traveling at the same speed there is a volume deficit to fill the ‘cavity’

This volume deficit creates an area of suction in the construction which allows a low pressure zone in the expansion for the construction static pressure to flow streamwise into and thus is converted to Dynamic Pressure

T0

at T1 under inertia

This suction will cease to occur when the inflection point is accelerated to 1.5V and fully providing with the required volume at the exit
Throat speed 2v, inflection point 1.5v, Exit 1V

allowing the normal slowing of the flow back to 1v and normal static pressure at the exit

As both of these only involve any exchange at the molecular level I think this change could occur at the speed of Propagation – Speed of sound ~ instantaneous

 

[256bits]

A funny shaped log is floating just submerged down a river flowing at 1 ms matching the current

I can see you have been thinking about this in depth.

What fluid is in the river?
Usually, we would assume it is water, but what if it is a river of molasses.
Would your analysis hold up?

 

[Quentin_C]

Hi thanks for the reply . Yes it puzzles me a lot as I think Continuity only reconciles the pressure variation it doesn't explain how it develops.

Yes I am keeping it to an inviscid flow, I am not considering viscosity.

 

[boneh3ad]

Is that really the case ?

Yes. It is kind of like Stokes' first problem, wherein an infinite flat plate is instantaneously started moving at some constant velocity. Even though the motion started instantaneously, the fluid still takes time to react.

Unless we are to somehow slow the whole of the flow in front or slow the flow of the stream behind .

Well, it would slow the flow down; it just wouldn't slow the whole flow down. If you imagine actually doing an experiment here, when you stop the log, you will see a large disturbance upstream of that log and, if it is close enough to the surface, you will likely even see a hydraulic jump. This is because, in nature, things don't happen instantaneously, and while the flow in the log develops, some of the incoming flow will be directed around the log instead of through it.

This leads me to conclude this must happen instantaneously.

It is probably quickly, but nothing is ever truly instantaneous (at least classically).

It also lead me to conclude that the pressure difference in this situation is in some ways a result not the cause (as I have seen often stated) of the increase in speed. At best it is concurrent and independent.

It's not really a cause/effect thing. In the governing equations for fluid flow, all of those parameters are codependent. One doesn't cause another, in general (though, for example, if you were to artificially change a pressure somewhere, you could view that as the pressure change causing a velocity change).

 

[Quentin_C]

Thanks for the reply

If I apply the information above then we are further away from the pressure/velocity variation we know develops, not closer

Yes I agree that, in an actual experiment, we would see disturbances (I have seen exactly what you describe in creeks) but as 256bits alluded to this, would be viscosity related. Inviscid flow we wouldn't see this as there is no force (drag force) on the fluid to slow it below 1ms

If indeed the flow above slows somehow (I am still unclear what the forces aside from viscosity could cause this disturbance , perhaps a resultant force like a pipe bend I don't know ? ) above the constriction then internally we now have less than (1ms< ).2A entering yet still 1ms.2A exiting under inertia
This may have slowed the acceleration component in the constriction but it has exacerbated the inertial suction of expansion due to our volume deficit.

Net result is the same net forces acting on the throat which are still to be resolved.

Additionally, if the flow above is slowed by either raising hydraulic head H+ or static pressure SP+ (SP in a pipe which is were I must apply this thinking) we also have in the free stream introduced a further gradient pg(h+) → pgh or (SP+)→ SP that must also be resolved

Can anyone poke a hole in the acceleration/suction explanation ?

Shall I restructure my question (so it is clearer what I am trying to understand) and repost ?

I really would love to understand the physical mechanism that causes the pressure/velocity variation to develop . Instantaneous might be misleading but as 900ms molecular speed of propogation is far in excess of our 1ms flow rate it would dominate the rate of change not the flow speed

Note: I also looked into Stokes first problem but the formula incorporates viscosity which makes sense in an inviscid flow the fluid velocity would not change as it encounters no (shear) force. How can I apply this to this inviscid scenario ?

 

[Quentin_C]

Hi I thought id repost a simplified scenario to try and get a broader audience to a question I really am stuck with

https://www.physicsforums.com/threads/instantaneous-bernoullis.867860/#post-5450743

I am trying to understand the physical mechanism that causes Bernoulli's pressure/velocity change
I get that it does happen just not the why.

The only way I can phrase this is by asking how it initially develops
A simplified scenario

A pipe fully filled withinitially static incompressible inviscid liquid with a piston on one end. The pipe has a constriction in it then an expansion

The piston is then subject to force (pressure difference) will have a front which initially propagates down the liquid at the speed of sound (~900ms) I I want to understand what happens when it initially encounters the constriction.Attempt at a solution
At the constriction the KE is shared with less and less mass in front - if we split into equal width sheets (fluid elements)

For equal KE the differences in mass will cause a differential acceleration F=m.a between each sheet /element - each will be accelerating at a faster rate than the one behind

This difference in "space" between elements in front (larger) than behind (smaller) allows an initially equal static pressure a greater mean free path/distance ahead than behind to flow into, by this mechanism is converted to dynamic pressure in the streamwise direction.

Bernoulli's variation is caused by the differences in mass causing increasing acceleration allowing a secondary directional conversion of static pressure to Dynamic

Thoughts ? Can someone poke a hole in this ?

 

[jartsa]

At the constriction the KE is shared with less and less mass in front

Well that's wrong, because kinetic energy of mass increases, and source of kinetic energy is not kinetic energy, but pressure energy.

If we knew how a trumpet works, then this problem might be solved, a trumped converts wind to pressure, and a trumpet in reverse mode converts pressure to wind. See how there's a sound wave going into a horn in your picture?

 

[Quentin_C]

Well that's wrong, because kinetic energy of mass increases, and source of kinetic energy is not kinetic energy, but pressure energy

Isn't that what I said ? that the kinetic energy of each layer is equal so shared over a smaller mass this means that each element is accelerating ? If you mean that the Kinetic Energy is increasing then yes that's what I am trying to understand . What physical mechanism causes this to occur at the expense of static pressure

If we knew how a trumpet works, then this problem might be solved

Are you saying that no one will be able to tell me why Bernoullis causes this change ? Just that it is observed and Continuity works to calculate the change ...without understanding how ?

 

[boneh3ad]

An inviscid flow would slow down as well. There is still a transient effect there and the log you cite has a nontrivial frontal area (from the POV of the flow), so there will be a force.

 

[Quentin_C]

An inviscid flow would slow down as well. There is still a transient effect there and the log you cite has a nontrivial frontal area (from the POV of the flow), so there will be a force.

If indeed the flow above slows somehow (I am still unclear what the forces aside from viscosity could cause this disturbance , perhaps a resultant force like a pipe bend I don't know ? ) above the constriction then internally we now have less than (1ms< ).2A entering yet still 1ms.2A exiting under inertia
This may have slowed the acceleration component in the constriction but it has exacerbated the inertial suction of expansion due to our volume deficit.

Ok so how do we get from a now slower flow to a flow that must speed up ? We have gone the wrong way ?

 

[boneh3ad]

Ok so how do we get from a now slower flow to a flow that must speed up ? We have gone the wrong way ?

Well the flow is only locally slower. There is still the free stream flow moving at 1 m/s (in your example) that will tend to bring the flow back to its 1 m/s state, and that is likely to occur quite rapidly. It should only be a very brief transient.

 

[Quentin_C]

Additionally, if the flow above is slowed by either raising hydraulic head H+ or static pressure SP+ (SP in a pipe which is were I must apply this thinking) we also have in the free stream introduced a further gradient pg(h+) → pgh or (SP+)→ SP that must also be resolved

Well the flow is only locally slower. There is still the free stream flow moving at 1 m/s (in your example) that will tend to bring the flow back to its 1 m/s state, and that is likely to occur quite rapidly. It should only be a very brief transient.

Ok looks like we are both talking about the same gradient and resolution above the constriction .So this localized gradient would just get us back to the same 1ms flow above I don't see how it is really relevant to the mechanism that causes the flow to go from 1ms to 2ms at the expense of static pressure?

That's all I want to know , not the continuity explanation nor the work explanation because they are just reconciliations of the pressure variation

They are not the How/ The mechanism of how this static is converted to DP

I see this same question asked over and over again in many forums and have never seen the 'How' actually explained'. I've given it a crack so interested in feedback'

Also I don't know who combined these threads its a mess, They are related but two different scenarios using different frames of reference done so that people might better understand what I am asking

 

[Quentin_C]

Additionally, if the flow above is slowed by either raising hydraulic head H+ or static pressure SP+ (SP in a pipe which is were I must apply this thinking) we also have in the free stream introduced a further gradient pg(h+) → pgh or (SP+)→ SP that must also be resolved

Well the flow is only locally slower. There is still the free stream flow moving at 1 m/s (in your example) that will tend to bring the flow back to its 1 m/s state, and that is likely to occur quite rapidly. It should only be a very brief transient.

Ok looks like we are both talking about the same gradient and resolution above the constriction .So this localized gradient would just get us back to the same 1ms flow above I don't see how it is really relevant to the mechanism that causes the flow to go from 1ms to 2ms at the expense of static pressure?

That's all I want to know , not the continuity explanation nor the work explanation because they are just reconciliations of the pressure variation

They are not the How/ The mechanism of how this static is converted to DP

I see this same question asked over and over again in many forums and have never seen the 'How' actually explained'. I've given it a crack so interested in feedback'

Also I don't know who combined these threads its a mess, They are related but two different scenarios using different frames of reference done so that people might better understand what I am asking

 

[boneh3ad]

The threads had to be combined because it was the same question posed two different ways. I don't know who combined them, but it was the right call.

As for the how, as I previously stated, pressure and velocity don't really have a cause and effect relationship. You can do something to change one and the other changes, or you can do something to change the other and the first one changes. In the case of something like a converging duct, the cause is continuity. Mass must be conserved, so the flow must speed up through the smaller section to avoid breaking this conservation law. This increase in kinetic energy must be balanced by a decrease in potential energy, which in this case is the static pressure. This holds for the case of an incompressible fluid, where the mass continuity equation and the momentum equation are all you need to solve for velocity and pressure.

If the flow is now assumed to be compressible (such as with higher-speed gases), then the conservation laws still hold, only now mass can be allowed to "pile up" (e.g. density can change locally) and you have extra equations to deal with in order to handle the added variable of density. Practically speaking, this means that temperature is now important because the momentum and continuity equations are now inextricably linked to the energy equation due to the compressibility of the flow. It just means there are more variables involved.

 

[rcgldr]

This might help, take a look at Molecular Scale Derivation in this NASA article:

http://www.grc.nasa.gov/www/k-12/airplane/bern.html

This seems to imply a frame of reference issue. From the fluid's frame of reference in a steady flow (before or after a Bernoulli transition), dynamic pressure is zero, so it would seem that the fluid's molecules only sense the original static pressure.

Consider a static port as used on some small aircraft. It is just a small hole in the surface of the aircraft that "hides" inside a boundary layer, and can "sense" the pressure of the ambient air, regardless of the aircraft's speed (assuming no mach speed related issues). The small hole is the end of a pipe that is flush mounted to the surface, with the pipe leading to a pressure sensing chamber. If such a static port was flush mounted in the narrow section of the pipe it would sense the lower pressure. If the static port was somehow setup so that it could move at the same speed as the stream in the narrow section of pipe, dynamic pressure would be zero, and it would sense the static pressure based on the total energy per unit volume of the fluid.

 

[rcgldr]

How do the Bernoulli conditions develop ...

Note that the reduced pressure in the narrower section has to somehow be created and maintained. In this case, the part of the pipe (log) that expands back to the original diameter is a pressure recovery zone, where the fluids pressure increases and the fluids speed decreases, sustaining the reduced pressure and higher speed in the narrow part of the pipe.

It's my guess, that most of the transition into Bernoulli flow starts at the trailing edge and moves its' way upstream towards the leading edge of the constricted pipe (log). Assume that the initial state is the fluid in the pipe is not moving (zero mass flow), this results in an increased pressure at the leading edge and a decrease in in pressure at the trailing edge, which starts the fluid to accelerate within the pipe. The initial flow into the expanding section senses reduced resistance and speeds up, which in turn reduces the pressure and increases speed further upstream within the narrow section, with this transition zone working it's way upstream until it reaches the upstream end of the constricted section of the pipe. Once the mass flow becomes steady (stops accelerating), then a Bernoulli like flow is established.

 

[mfig]

I think it is too difficult to visualize what actually happens in the transition, and this is easy to understand because of the nonlinear equation that describes the situation. If we keep the first 4 assumptions required for Bernoulli's equation

• incompressible flow
  
• inviscid flow
  
• along a streamline
• inertial reference frame
• steady state

and if I have not made an error somewhere, then the governing equation for the situation is given:

$\vec{\nabla}\left( \frac{V^2}{2} + gy + \frac{P}{\rho}\right) = -\frac{\partial \vec{V}}{\partial t}$One can see Bernoulli lurking there in the parenthesis, but it is hard to understand what is going on physically as the system evolves towards steady state. It would be interesting to see this equation solved in order to watch the transition.

 

[jartsa]

Isn't that what I said ? that the kinetic energy of each layer is equal so shared over a smaller mass this means that each element is accelerating ? If you mean that the Kinetic Energy is increasing then yes that's what I am trying to understand . What physical mechanism causes this to occur at the expense of static pressure

Accelerating mass does not absorb kinetic energy, at least not in this case, because nothing is losing any kinetic energy. But accelerating mass absorbs momentum, and another way to say that is to say that accelerating mass exerts a force.

So, all the parcels of accelerating mass exert a force on the piston, through the fluid, the result of this is that the fluid between the piston and accelerating mass is under pressure.

(See first two pictures in post #8)

Although the force-exerting accelerating parcels seem to be kind of connected in series, the force on the piston is the sum of forces exerted by all the parcels. And that's because ... well I guess the accelerating parcels of force-exerting fluid are like accelerating railroad engines connected in series. Series-connected railroad engines exert a force on the rails, series-connected accelerating parcels of fluid exert a force on the piston.

 

[boneh3ad]

If we keep the first 4 assumptions required for Bernoulli's equation

• incompressible flow
  
• inviscid flow
  
• along a streamline
• inertial reference frame
• steady state

Actually, not all of those are required for Bernoulli's equation to be valid. For example, if the flow is irrotational (usually true of inviscid flows), then there is nothing that requires Bernoulli's equation to be used along a streamline. On the other hand, if the flow is rotational, then it must be used along a streamline because the total pressure changes from one streamline to the next.

and if I have not made an error somewhere, then the governing equation for the situation is given:
$$\vec{\nabla}\left( \frac{V^2}{2} + gy + \frac{P}{\rho}\right) = -\frac{\partial \vec{V}}{\partial t}$$
One can see Bernoulli lurking there in the parenthesis, but it is hard to understand what is going on physically as the system evolves towards steady state. It would be interesting to see this equation solved in order to watch the transition.

This works, though more typically, since the flow is generally assumed to be irrotational, it is more convenient to express the velocity in terms of a scalar potential, so $\vec{v} = \nabla\Phi$. In that case, the gradient can integrated away to give
$$\dfrac{\partial \Phi}{\partial t} + \dfrac{v^2}{2} + \dfrac{p}{\rho} + gz = F(t).$$
In this case, $F(t)$ is constant everywhere for a given point in time in the fluid, but may vary with time. You can of course replace the other $v^2$ in there with $|\nabla\Phi|^2$ but it doesn't really matter. This form is slightly more helpful in mentally visualization what is going on, but it still not easy to solve like the steady equation is.

 

[Quentin_C]

Thanks for all the replies

nothing is losing any kinetic energy.

how is that so? if we go down to the molecular level and we say that the piston depresses just 1 molecular depth

then once the first layer moves 1 layer to the right it is in its final position (with a velocity of zero) KE~of zero it has now passed its KE energy on to the next layer and so on .
This doesn't hold when mass changes ,Once it hits the constriction it has smaller mass for same force we must have differing acceleration

Looking at it from momentum. Momentum is conserved ? So for a smaller mass we must have a larger velocity. Acceleration is Vfinal -VInitial so acceleration is different
Assuming a frictionless environment of perfectly elastic collisions within a incompressible fluid.

), this results in an increased pressure at the leading edge and a decrease in in pressure at the trailing edge, which starts the fluid to accelerate within the pipe

Sorry can you explain where you mean by leading and trailing edge ? Are you meaning like on a sound wave or equating these terms to physical locations in the pipe ?

Mass must be conserved, so the flow must speed up through the smaller section to avoid breaking this conservation law. This increase in kinetic energy must be balanced by a decrease in potential energy, which in this case is the static pressure. This holds for the case of an incompressible fluid, where the mass continuity equation and the momentum equation are all you need to solve for velocity and pressure

In the initial log example all I am trying to establish (in a very similar situation to the log) is if the pressure/speed varys immediately due to some mechanism or simply develops at the speed of the flow (as the 1ms flow is "flushed" out of the constriction ) - both Continuity/conservation and the flow developing answers can't be right.
If things must be then they must be at all scales of time . The old physics is time invariant thingy

 

[rcgldr]

It's my guess, that most of the transition into Bernoulli flow starts at the trailing edge and moves its' way upstream towards the leading edge of the constricted pipe (log).

Can you explain where you mean by leading and trailing edge?

As mentioned in my post, leading edge is the upstream edge of the pipe, trailing edge would be the downstream edge of the pipe. The leading edge would experience increased pressure related to impact or dynamic pressure, the trailing edge would experience reduced pressure due to drag related effects.

Are you meaning like on a sound wave or equating these terms to physical locations in the pipe ?

Pressure impulses travel at the speed of sound in water, but the inertia of the water means the actual acceleration from the initial state of zero velocity everywhere to the steady flow state of velocities takes much longer than the time for a sound wave to travel that distance. The rate of acceleration within the narrow section would be greater than the rate of acceleration in the wider sections. Since the initial state has higher pressure at the leading edge and lower pressure at the trailing edge of the entire pipe, I'm thinking that the lower pressure within the narrow section starts at the trailing edge, and quickly works its way upstream to the leading edge of the narrow section. I'm not aware of an article that would describe what happens during the transition from zero flow to steady state flow within a constricted pipe, so this is conjecture on my part, in an attempt to explain what was asked for in the earlier posts.