How Do Temperatures Change in Insulated Helium-Filled Cylinders?

[koolkuzz]

Thermodynamics problem...

I am stuck on the following problem:

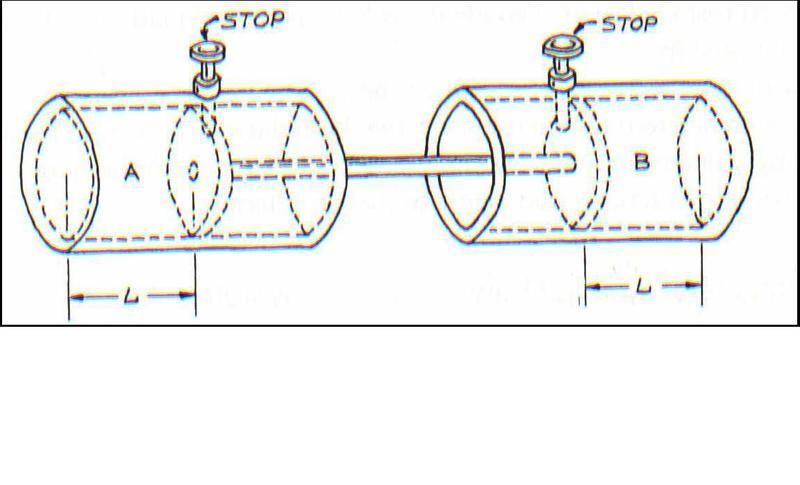
"Two well-insulated cylinders are placed as shown in Figure . The pistons in both cylinders are of identical construction.
The clearances between piston and wall are also made identical in both cylinders. The pistons and the connecting rod are
metallic.
Cylinder A is filled with gaseous helium at 2 bar and cylinder B is filled with gaseous helium at 1 bar. The temperature
is 300 K and the length L is 10 cm. Both pistons are only slightly lubricated.
The stops are removed. After all oscillations have ceased and the system is at rest, the pressures in both cylinders are,
identical.
1. Assuming that the gases are ideal with a constant Cv and assuming that the masses of the cylinder and pistons are
negligible (any energy changes of pistons and cylinders can be neglected), what are the final temperatures?
2. Consider the situation with well-insulated pistons and connecting rods of low thermal conductivity. What are the
final temperatures after the oscillations have ceased and the pressures have equalized?"

Any help would be greatly appreciated.

 

[koolkuzz]

I have tried to solve part 1 of the question,
I got the following so far:

When the stops are removed, then the system will keep hitting the side back and forth.
Hence work done by one piston will be equal to the work done on the other piston:
W=-W (negative since its the other direction)
since system is insulated, dU=dW and hence
U1=-U2
The internal energy U = CvdT and inputting this into above eq'n:
CvdT = -CvdT
Since the question assumes constant Cv, then:
dT = -dT
Change in temp in one cylinder will equal change in temperature in the second cylinder.

Thats all i have so far....not sure though

Anyone have any idea if I am on the right path, help needed!

 

[Gokul43201]

In Q1, what is the significance of a metallic connecting rod ?

 

[koolkuzz]

The metallic rod is basically used to transfer any heat produced from the oscillations from one piston to the other.

PArt 2 should be considered as an adiabatic reversible process due to the low thermal conductivity of the rods.

 

[Andrew Mason]

I have tried to solve part 1 of the question,
I got the following so far:

When the stops are removed, then the system will keep hitting the side back and forth.
Hence work done by one piston will be equal to the work done on the other piston:
W=-W (negative since its the other direction)
since system is insulated, dU=dW and hence
U1=-U2
The internal energy U = CvdT and inputting this into above eq'n:
CvdT = -CvdT
Since the question assumes constant Cv, then:
dT = -dT
Change in temp in one cylinder will equal change in temperature in the second cylinder.

The total internal energy of the system does not change. The work done on cylinder 2 is:

W = \int_{vi}^{vf} Pdv = \int_{vi}^{vf} \frac{nRT}{V}dv

If the two cylinders are thermally connected, as in the first question, what can you say about the temperature?

The second question is a little trickier. The total energy is conserved but this time the internal energy of the gas in each cylinder changes by the work done by or to it.

The incremental decrease in internal energy in cyl1 will be dU_1 = n_1CvdT_1 = PdV_1 and incremental increase in cyl2 is dU_2 = n_2CvdT_2 = PdV_2. From that, keeping in mind that PdV is the same in each case and total energy does not change, you should be able to determine the change in temperature.

AM

 

[koolkuzz]

I'm slighlty confused now, for Part A: what your trying to say is that the temperature in both cylinders are the same (300k), is that right?

For part B, what answer do you get for the temperatures?

 

[Andrew Mason]

I'm slighlty confused now, for Part A: what your trying to say is that the temperature in both cylinders are the same (300k), is that right?

What do you think?

For part B, what answer do you get for the temperatures?

Well, see if you can work it out:

(1)nC_vT_1 + 2nC_vT_2 = U_f = U_i = 3nC_vT_i and

(2)nC_v(T_1-T_i) = 2nC_v(T_2-T_i)

and, using PV/T = nR = constant, you should get:

(3)\frac{V_{1f}}{V_{2f}} = \frac{T_{2}}{T_{1}}AM

 

[Andrew Mason]

and, using PV/T = nR = constant, you should get:

(3)\frac{V_{1f}}{V_{2f}} = \frac{T_{2}}{T_{1}}

I misled you on this. If the connecting rod does not conduct heat, there is no transfer of heat from either chamber so this appears to be an adiabatic process, to which the adiabatic condition applies:

PV^\gamma = constant

So you should get:

\frac{V_2^{\gamma-1}}{V_1^{\gamma-1}} = \frac{T_1}{T_2} = and

V_1^{\gamma} = 2V_2^{\gamma}

This should enable you to solve it.

AM