kmiller
- 14
- 0
displacement problems...help!
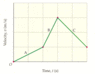
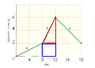
A person on horseback moves according to the velocity-versus-time graph shown in Figure 2-29. (The vertical axis is marked in increments of 2 m/s and the horizontal axis is marked in increments of 4 s.) Find the displacement of the person for each of the segments A, B, and C.

Find
m (A)
m (B)
m (C)
Homework Statement
A person on horseback moves according to the velocity-versus-time graph shown in Figure 2-29. (The vertical axis is marked in increments of 2 m/s and the horizontal axis is marked in increments of 4 s.) Find the displacement of the person for each of the segments A, B, and C.
Find
m (A)
m (B)
m (C)