theoriginalh
- 5
- 0
Hi there, I'm struggling with a question that I've been given regarding the force on a bend in a pipe, and I wondered if any of you guys could help me out with a few clues. The question is as follows:
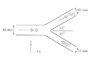
A contracting pipe bend turns water through 135° (In a horizontal plane) before discharging it to the atmosphere. The inlet diameter is 80mm and the outlet diameter is 60mm. The volumetric flow rate is 20 Ls
a) Neglecting energy losses, calculate the upstream pressure and the magnitude and direction of the force on the bend.
b) If the upstream pressure is actually 24kPa, calculate the loss of head in the pipe bend.
Diagram below
I really don't know where to get started with this problem, so any help would be welcome.
Thanks
A contracting pipe bend turns water through 135° (In a horizontal plane) before discharging it to the atmosphere. The inlet diameter is 80mm and the outlet diameter is 60mm. The volumetric flow rate is 20 Ls
a) Neglecting energy losses, calculate the upstream pressure and the magnitude and direction of the force on the bend.
b) If the upstream pressure is actually 24kPa, calculate the loss of head in the pipe bend.
Diagram below
I really don't know where to get started with this problem, so any help would be welcome.
Thanks