questionable
- 3
- 0
Homework Statement
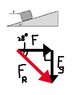
A 90 kg box is pushed by a horizontal force F at constant speed up a ramp inclined at 28°, as shown. Determine the magnitude of the applied force:
a. when the ramp is frictionless.
b. when the coefficient of kinetic friction is 0.18.
Homework Equations
F= ma, Ffr = μk * Fn
The Attempt at a Solution
Everywhere I look online I keep getting told that for part (a) I need to do sin28 * 882N (i.e. sin28 * mg) but I have NO idea why. Could somebody draw me a picture of the vector decomposition because I really really do not understand why you'd multiply.
For part (b) my course hasn't even taught us about kinetic friction yet, but through looking around I've found out that Ffr = μk * Fn. So once I've found the force of friction, what do I do with it?
Thanks for any help...