How Do You Calculate Tension in Multiple Supporting Wires?

[PokeFan]

Homework Statement

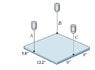
A uniform steel plate 18 in. square weighing 87.8 lb is suspended in the horizontal plane by the three vertical wires as shown. Calculate the tension in each wire ((a)TA , (b)TB, and (c)TC).

Homework Equations

\SigmaM=0

The Attempt at a Solution

both A and B are 9 in. from the x axis
C is on the x axis, so A and B have to be equal or it would rotate about x axis
A+B+C=87.8 or it would move in or out of the page

 

[pongo38]

Good start. You have identified an axis about which moments must be equal. Actually ANY axis could be chosen, and the moments about that axis would have to balance. Why not choose an axis passing through two of the unknown tensions?

 

[PokeFan]

Thank you, I solved it using the Sum of the moments about the X and Y axis and the Sum of the forces about the Z.

 

[pongo38]

Ah yes but did you check it by taking moments about some other axis? (always wise to do that)