How Do You Calculate the Mass of a Pulley in a Physics Problem?

  • Thread starter Thread starter theknownothing
  • Start date Start date
  • Tags Tags
    Mass Pulley
AI Thread Summary
To calculate the mass of a pulley in a physics problem involving two blocks and a rope, one must consider the torque acting on the pulley and its angular acceleration. The downward acceleration of the 44.0 kg block is half of the acceleration due to gravity, indicating that the tension in the rope differs on each side of the pulley. The relevant formulas include the relationship between linear acceleration, mass, and gravity, as well as the rotational inertia of a solid cylindrical disk. By determining the torque and angular acceleration, one can derive the mass of the pulley. Understanding these concepts is crucial for solving the problem effectively.
theknownothing
Messages
10
Reaction score
0
Hi people again, sorry to not have done extensive searching in the forum for a problem like this but I need some help ASAP.

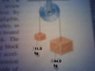
By means of a rope whose mass is negligible, two blocks are suspended over a pulley, as the drawing shows. The pulley can be treated as a uniform solid cylindrical disk. The downward acceleration of the 44.0 kg block is observed to be exactly one-half the acceleration due to gravity. Noting that the tension in the rope is not the same on each side of the pulley, find the mass of the pulley.


Thank you guys!
 

Attachments

  • pulley.jpg
    pulley.jpg
    6.5 KB · Views: 780
Last edited:
Physics news on Phys.org
I am not sure which formula to use to find the mass of the pulley since the accelartion is

a=m2-m1/m1+m2 * gravity that would give me the accel if it was a massless pulley.

any help appreciated.
 
I can't see your graph... but i think i can guess how its look like
since you are new here, just want to let you know our rule here does not allow me giving you the full solution... I can only give you some hints and you got to work out the problem yourself

hints:
1. what is the touqe acting on the pulley?
2. what is the angular acceleration for the pulley
3. after you have the above numbers and the rotational inertial for a disk, you should able to figure out what the mass is...
 
alright thanks got the problem!
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Newton's Second Law (Pulley Sustem)
Replies
3
Views
2K
Experimental Design: Pulley and Mass Hangers
Replies
30
Views
3K
What's my mistake in this problem in dynamics involving pulleys?
Replies
35
Views
3K
Angular acceleration of an atwood pulley
Replies
8
Views
4K
Angular Acceleration and Linear Acceleration of a Pulley
Replies
4
Views
2K
How Do You Calculate the Angular Motion of a Pulley System?
Replies
15
Views
2K
Mass and pulley system (Rotational Dynamics)
Replies
9
Views
2K
Find when the acceleration is 0
Replies
15
Views
2K
Acceleration of a Mass in a Pulley System
Replies
6
Views
3K
Projectile Motion with Pulley System
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top