How Do You Calculate the Maxwell Stress Tensor Between Cylindrical Shells?

AI Thread Summary
To calculate the Maxwell stress tensor between two nonconducting cylindrical shells surrounding current-carrying wires, one must first determine the electric and magnetic fields at the midpoint between the shells. The electric field is influenced by the charge per unit length of the shells, with the x shell having a positive charge and the y shell a negative charge. The relevant equation for the Maxwell stress tensor is T_ij = ε₀(E_iE_j - δ_ijE²) + (1/μ)(B_iB_j - δ_ijB²). The user seeks assistance in finding the i and j components of the electric and magnetic fields necessary for this calculation. Understanding these components is crucial for accurately computing the Maxwell stress tensor in this scenario.
tomfrank
Messages
37
Reaction score
0

Homework Statement


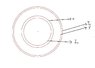
x and y are nonconducting cylindrical shells. Both cylindrical shells are surrounding long wires that are carrying current. the x shell out of the page and the y shell into the page.
x radius has a charge per unit length = to +\lambda
y radius has a charge per unit length = to -\lambda
I need to calculate the maxwell stress tensor at a midway between x and y. (from the picture)

Homework Equations



Tij =\epsilono(EiEj-\deltaijE2)+(1/\mu)(BiBj-\deltaijB2)

The Attempt at a Solution



How do I exactly found the i and j component of the magnetic and electric field?
 

Attachments

  • cylinder.jpg
    cylinder.jpg
    22.7 KB · Views: 404
Last edited:
Physics news on Phys.org
can anyone help me?
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »

Similar threads

How Does Gauss' Law Apply to an Insulated Cylindrical Shell and Rod System?
Replies
5
Views
2K
Understanding the Maxwell Stress Tensor
Replies
3
Views
4K
Heat transfer through a cylindrical shell
Replies
3
Views
3K
A Stress-energy tensor of a rotating rod
Replies
21
Views
3K
Stress and Strain tensors in cylindrical coordinates
Replies
3
Views
3K
How Does Maxwell's Stress Tensor Apply to an Infinite Parallel Plate Capacitor?
Replies
2
Views
5K
How Do You Calculate Shear Stress in a Coronary Artery?
Replies
2
Views
2K
Coaxial cable conductors with dielectric: polarization of charge
Replies
10
Views
2K
Maxwell Stress Tensor Homework: Find E & B Field Components
Replies
3
Views
3K
A Stressing Over Stress Tensor Symmetry in Navier-Stokes
Replies
2
Views
2K

Hot Threads

Recent Insights

Back
Top