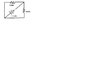dukeedee
- 2
- 0
I tried finding this same problem somewhere in the forums here but I couldn't find a similar one, its getting the best of me! I have a problem with a square and a line going diagonal from corner to corner, with a 1.5v battery on the diagonal and on the top side a 4ohm resistor and 6ohm resistor on the other side. So the battery intersects the corner with a resistor on either side of the corner. Would it just be two in parallel so (1/4 + 1/6)^-1 = 2.4ohms? I cannot figure it out, help please!