How Do You Calculate Triangle Peak Equations in MATLAB?

[Spoolx]

Hi,
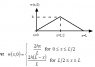
I am working on some MATLAB for my engineering classes and I need help with understanding a given diagram.

In the attached diagram, I need help understanding how we determined the equations

For example, I would like to know the equations for a triangle with the peak at 2/3L

I know the equations would be from

0<=x<=2/3L
2/3L<=x<=L

but I need help creating the equations.

Thanks!

 

[Chestermiller]

If you have two points on a straight line at (0,0) and (L/2,h) and you are asked to determine the equation of that line, do you know how to determine it, say, in slope-intercept form?

Same thing for the other line through the points (L/2,h) and (L,0).

Chet

 

[Spoolx]

Okay that makes sense, but when I solve like that I end up with a negative in the second equation and still not sure where the x comes in
m1=h/L/2 or 2h/L
m2=-h/L/2 or -2h/L

I apply that to my 2/3 triangle

m1=3h/2L
m2=-3h/L
both my m2's are negative but the given equation has the original m2 as positive.

btw thanks for the tip so far

EDIT:

actually give me a minute before you answer, i think I need to plug it into y=mx+b

 

[Spoolx]

So my actual problem has the triangle peak at 3/4L and the peak is represented by hplease verify my equations
slope 1 = 4h/3L
slope 2 = -4h/L

equation 1 = 4hx/3L
equation 2 = -4hx/L + 12h or (4h(3L-x))/L

Please verify I did it correctly

Thank you

 

[Chestermiller]

So my actual problem has the triangle peak at 3/4L and the peak is represented by h


please verify my equations
slope 1 = 4h/3L
slope 2 = -4h/L

equation 1 = 4hx/3L
equation 2 = -4hx/L + 12h or (4h(3L-x))/L

Please verify I did it correctly

Thank you

You can verify it yourself. In eqn 2, if you substitute x = L, do you get y = 0?

Chet