DoomBringer2
- 4
- 0
1. Hello everyone, I am having some trouble determining precise phase shifting by observing the graphs.
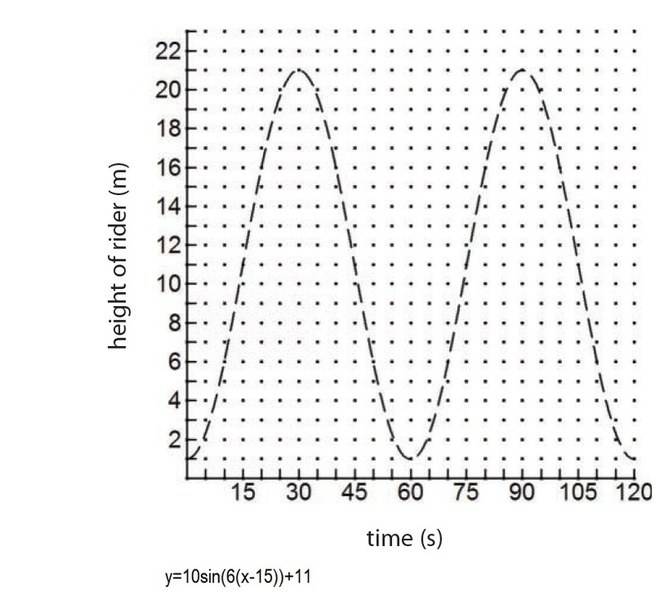
book says this graph has horizontally shifted to the right by 15 units. How was this determined? I can't figure it out!
second this graph:
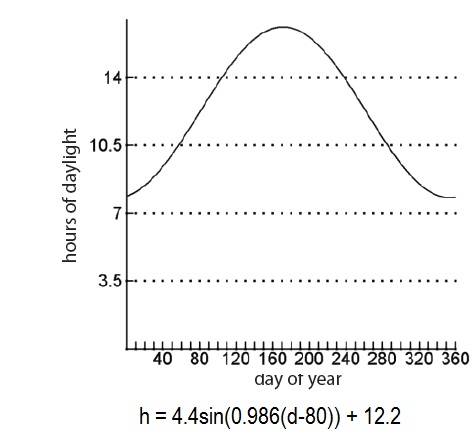
Says the graph was shifted 80 units to the right but again how is this determined? Please help thnx
book says this graph has horizontally shifted to the right by 15 units. How was this determined? I can't figure it out!
second this graph:
Says the graph was shifted 80 units to the right but again how is this determined? Please help thnx