How Do You Solve Complex Pulley System Problems in Physics?

[HobieDude16]

HELP! pulley problems, can't figure formula out...

ok, for physics here at uf, there are 2 problems in this homework i just can't figure out, and I am sure I am just being stupid, but can anyone help me? here they are...

In Figure 5-50, three ballot boxes are connected by cords, one of which wraps over a pulley having negligible friction on its axle and negligible mass. The masses are mA = 22.0 kg, mB = 40.0 kg, mC = 18.0 kg.

Fig. 5-50

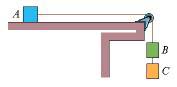
(a) When the assembly is released from rest, what is the tension in the cord that connects boxes B and C?
N
(b) How far does box A move in the first 0.250 s (assuming it does not reach the pulley)?
m

and the other is

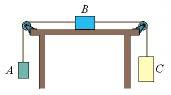
Figure 5-55 shows three blocks attached by cords that loop over frictionless pulleys. Block B lies on a frictionless table; the masses are mA = 7.00 kg, mB = 8.00 kg, mC = 10.5 kg. When the blocks are released, what is the tension in the cord at the right?
N

 

[HobieDude16]

i tried for about 3 hours to get these, but i can't seem to figure out what formulas to use, does anyone have any ideas?

 

[GingerBread27]

I have the same problems lol, and no clue how to do them either. I hope someone can help. :)

 

[HobieDude16]

yeah, i can't figure it out, but apparently nobody else on this board can either, nor any of my friends... so i don't think I am going to be able to figure them out

 

[GingerBread27]

Yeah no one i know can solve these problems either.

 

[HobieDude16]

ha, i got the help from a car forum... funny how a car forum would help me before a physics help forum...!

 

[GingerBread27]

how did you do it?

 

[Pyrrhus]

Actually, if you both show your work... then people will be more willing to help out!. Remember we're not here to do your homework, but we will gladly provide hints, so you can do it.

 

[HobieDude16]

ah, well, i just asked for some formulas that yall thought would work, not to just give me the answers... which is what the other forum did, and i figured out how to use them, and got the answer!

 

[HobieDude16]

With the same argument I used in the first one, calcualte the acceleration of the system, do a free body diagram of the body supported by the string in question. In b)

F = ma = (-7kg+10.5kg) *g = 3.5g

Total mass = 25.5 kg

So acceleration of system = g*3.5/25.5

Thus with a downward force of mg on block C (10.5kg) the rest of the force is the tension = 10.5kg*g*22/25.5 = 88.9N

thats how they explained the 2nd one to me, makes a lot of sense when you think about it... and yeah, that's using the numbers from my problem, so if yours are different, change them

 

[HobieDude16]

As for rate of acceleration, the same applies. The driving force is the unsupported mass, i.e. (Mass B + Mass C)*g, but its actually accelerating an additonal mass that is not falling also, so it doesn't accelerate at g.

Acceleration = Force/Mass = (Mass B + Mass C)*g / (Total Mass)

= g * 58/80

Then s=ut+0.5*a*t^2 and u = 0

Distance traveled with t = 0.250s...

s = 0.5 * accelerationfromabove * 0.250^2 = 0.22m

theres part b of the first one

 

[HobieDude16]

i think this is part a too
We know my g*58/80 is the correct acceleration because it answered section b. Think of block C as a free body diagram. It has force mg downwards obviously, but is only moving downwards at g*58/80. Therefore IT MUST have an upward force of mg*22/80 provided by the string to make it balance.
k, I am leaving now, hope it helps

 

[1stcool]

hey, hobie, i got same problem, i figure out part b, but wat about part a, i am still confuse about it, thx.