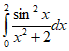How Do You Solve Tricky Integrals in AP Calculus?

[smodak]

Evaluate

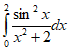
What I tried so far is to break the denominator as (1+Cos2x). The integral of 1/(x^2+2) can be done with substituting x = sqrt(2)u and will evaluate to a constant times arctan (x/sqrt(2)) but I have no idea how to evaluate the rest. This is calculus AP (with real numbers only). My daughter asked me about this problem and I am stuck :). Any help is much appreciated.

 

[Charles Link]

It looks quite difficult. A numerical integration (estimate) with increments $\Delta x =.001$ or smaller would be straightforward, but I don't see how to get an exact answer.

 

[Ray Vickson]

It looks quite difficult. A numerical integration (estimate) with increments $\Delta x =.001$ or smaller would be straightforward, but I don't see how to get an exact answer.

It involves non-elementary functions. Maple evaluates the indefinite integral as
1/2*arctan(x)+1/4*Si(2*x-2*I)*sinh(2)+1/4*I*Ci(2*x-2*I)*cosh(2)+1/4*Si(2*x+2*I)*sinh(2)-1/4*I*cosh(2)*Ci(2*x+2*I),
where Si and Ci are the so-called "sine" and "cosine" integrals, defined as
$$\text{Si}(x) = \int_0^x \frac{\sin(t)}{t} \, dt,$$
and
$$\text{Ci}(x) = \gamma + \ln (x) + \int_0^x \frac{\cos(t) -1}{t} \, dt, $$
where $\gamma$ is Euler's constant.

 

[MidgetDwarf]

Evaluate View attachment 215463

What I tried so far is to break the denominator as (1+Cos2x). The integral of 1/(x^2+2) can be done with substituting x = sqrt(2)u and will evaluate to a constant times arctan (x/sqrt(2)) but I have no idea how to evaluate the rest. This is calculus AP (with real numbers only). My daughter asked me about this problem and I am stuck :). Any help is much appreciated.

Can you give the name of the section were this problem is given? I am thinking it has to do with series.

 

[smodak]

Can you give the name of the section were this problem is given? I am thinking it has to do with series.

This is given in the section of the 2nd fundamental theorem of calculus. I actually wrote to the person who created this problem. She just wrote to me that this she meant for it to be solved with a calculator (TI-84).