How Does a Particle Inside a Rolling Cylinder Affect Its Motion?

[Azael]

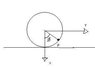
As in the attached picture.
A cylindrical shell with mass M can roll without gliding on a horizontal plane

In the cylindrical shell a particle ,p, with mass m can glide without friction.

At the beginning there is no motion and the angle to the particles position is \phi=\frac{\pi}{2}


I am suposed to find the movement of the center of the circle as a function of the angle \phi

Im not sure how I should start.

The potential energy of the system is, if I place the plane of reference on the level of the horizontal plane.

V=mgR(1-cos\phi)

Now this problem obviously only has one degree of freedom and that is the angle \phi

But if I want to construct a lagrangian I must use two degres of freedom. The rotation angle of the cylinder \alpha and the angle to the particle p \phi. Because I don't know how \alpha and \phi are connected. Is this the correct thinking?

In that manner I get this equation

L=T-V=\frac{3}{4}MR^2\dot{\alpha}^2+\frac{1}{2}m[\dot{\alpha}^2 R^2 + R^2\dot{\phi}^2 + \dot{\alpha}^2 R^2 sin\phi ] - mgR(1-cos\phi )

Should I use this and solve the two lagrande equations

\frac {d}{dt} \frac{dL}{d\dot{\alpha}}-\frac{dL}{d\alpha}=0

\frac {d}{dt} \frac{dL}{d\dot{\phi}}-\frac{dL}{d\phi}=0

Im not sure if this will give me any answere though? It feels like I should express \alpha in \phi before I even do the lagrangian. Am I on the right track?

 

[Azael]

I assume that I in the same manner can get the hamiltonian since its a conservative force situation and holonomic constrains.

H=T+V=\frac{3}{4}MR^2\dot{\alpha}^2+\frac{1}{2}m[\dot{\alpha}^2 R^2 + R^2\dot{\phi}^2 + \dot{\alpha}^2 R^2 sin\phi ] + mgR(1-cos\phi )

But I am not quite sure what I would do with that one either. I know that

\dot{\alpha}=\frac{dH}{dP_{\alpha}}
and
-\dot{P_{\alpha}}=\frac{dH}{d\alpha}

But that doesn't seem to be much help either??

 

[silimay]

I don't know...I wish I could help...

It seems like you really do need two generalized coordinates. I mean, the particle is free to move; it doesn't seem like it is constrained in any way such that \phi and \alpha would be related.

 

[Hargoth]

I think that there is an error in your Lagrangian: Since you are interested in the movement of the cylinder and watch it in the "labatory system", so to say, you can't say that the velocity of the particle in y-direction is R \dot \phi \cos(\phi). \phi is fixed in the "cylinder system", so you have you add the y-velocity of the cylinder. If you square this, you should get a "mixed term" so that the both velocities are related.

 

[Azael]

I managed to solve it. my expression for the Y position of the particle was

Rsin\phi + R\alpha

So velocity was

R\dot{\phi}cos\phi + R\dot{\alpha}

I used the fact that the conjugated momentum is constant for the alpha coordinate since there is no alpha, just alpha dot, dependence :) tricky problem.