kenau_reveas
- 39
- 0
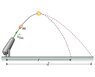
A mortar fires a shell of mass m at speed v0. The shell explodes at the top of its trajectory (shown by a star in the figure) as designed. However, rather than creating a shower of colored flares, it breaks into just two pieces, a smaller piece of mass 1/5 m and a larger piece of mass 4/5 m. Both pieces land at exactly the same time. The smaller piece lands perilously close to the mortar (at a distance of zero from the mortar). The larger piece lands a distance d from the mortar. If there had been no explosion, the shell would have landed a distance from the mortar. Assume that air resistance and the mass of the shell's explosive charge are negligible.
Find the distance d from the mortar at which the larger piece of the shell lands.
Express d in terms of .
Find the distance d from the mortar at which the larger piece of the shell lands.
Express d in terms of .