unscientific
- 1,728
- 13
Length Contraction "Ether wind"
Due to the ether wind, anything that moves along it is "contracted".
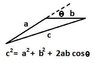
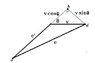
Taking L1 to be contracted length,
(L1)2
= (L1x)2 + (L1Y)2
= (L10,X/γ)2 + (L10,Y)2But what they wrote is the opposite..
Homework Statement
Due to the ether wind, anything that moves along it is "contracted".
The Attempt at a Solution
Taking L1 to be contracted length,
(L1)2
= (L1x)2 + (L1Y)2
= (L10,X/γ)2 + (L10,Y)2But what they wrote is the opposite..
Attachments
Last edited: