nickyfernandezzz
- 18
- 2
Homework Statement
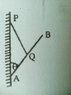
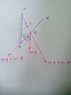
The original question was to find the value of the angle between PA and AB. I have a certain idea regarding how to find it, but first I have to identify all forces acting on the system and their directions. So, I would be grateful if someone can explain how the frictional force acts between PA
and AB.
MY ATTEMPT.
I got a start by marking the forces acting on the system but I can't figure out the direction of frictional force.