How Does Inviscid Flow Behave Around a Submerged Cone?

[member 428835]

Hi PF!

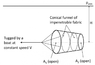
Some classmates and I were talking about the streamlines around a submerged cone being pulled at a velocity $V$. The picture is attached. Can someone shed some light on the streamlines of this flow, assuming it is inviscid? I take a frame of reference that moves with the cone.

Specifically, would the flow at station 2 be uniform vertically, or would the flow be faster at the exit port forever? Would the streamline profiles be straight upon exit or would they bend a little?

Any insight is greatly appreciated!

 

[Chestermiller]

What do you think the streamline pattern would look like?

 

[member 428835]

What do you think the streamline pattern would look like?

I think the streamlines outside $A_1$ will wrap around the cone and at station 2 all be flat. I think the streamlines in the cone, at station 2, will all be flat too. Before station 2 and in the cone I think the streamlines will adhere to the shape of the wall and condense. I think these streamlines will exit condensed relative to those outside the cone. Since the flow is inviscid, I think streamlines beyond station 2 directly behind $A_2$ will always be closer together than those outside $A_2$. So a sort of jet.

 

[Chestermiller]

I think the streamlines outside $A_1$ will wrap around the cone and at station 2 all be flat. I think the streamlines in the cone, at station 2, will all be flat too. Before station 2 and in the cone I think the streamlines will adhere to the shape of the wall and condense. I think these streamlines will exit condensed relative to those outside the cone. Since the flow is inviscid, I think streamlines beyond station 2 directly behind $A_2$ will always be closer together than those outside $A_2$. So a sort of jet.

Any chance of a diagram?

 

[member 428835]

Any chance of a diagram?

Totally, I've attached one. I've tried drawing all the streamlines equidistant before station 1. Notice after station 2 they are closer together behind $A_2$ then before. Do you agree with this sketch?

 

[Chestermiller]

Totally, I've attached one. I've tried drawing all the streamlines equidistant before station 1. Notice after station 2 they are closer together behind $A_2$ then before. Do you agree with this sketch?

I think that further downstream (after station 2), they will become equidistant again.

 

[member 428835]

I think that further downstream (after station 2), they will become equidistant again.

What would cause the streamlines to separate after station 2?

 

[Chestermiller]

Do you believe that the stream function satisfies Laplace's equation for inviscid flow?

What causes the stream lines to even out again downstream of flow over a cylinder?

 

[member 428835]

Do you believe that the stream function satisfies Laplace's equation for inviscid flow?

I believe the streamfunction does provided the flow is also incompressible (which we assume it is) so yes, I believe the streamfunction $\psi$ follows $\nabla^2\psi=0$.

What causes the stream lines to even out again downstream of flow over a cylinder?

Yea, I'm not sure about this. Any help?

Also, and I know this is off topic a little, but when deriving Bernoulli's equation from Navier Stokes, how do we know it is only valid along a streamline? At the very end of my derivation, assuming Newtonian, incompressible, inviscid, irrotational flow I have $\nabla(\partial_t \phi + |\vec{u}|^2/2+p/\rho + g z) = \vec{0} \implies \partial_t \phi + |\vec{u}|^2/2+p/\rho + g z = const.$ where I think the constant implies something about which streamline you're on. Also, $\vec{u}=\nabla \phi$.

 

[Chestermiller]

I believe the streamfunction does provided the flow is also incompressible (which we assume it is) so yes, I believe the streamfunction $\psi$ follows $\nabla^2\psi=0$.

Well, if the stream function satisfies Laplace's equation and the streamlines become parallel at large x, then $\partial \psi /\partial x=0$. Therefore, we are left with $\partial^2\psi /\partial y^2=0$. That automatically gives equal streamfunction spacing.

Yea, I'm not sure about this. Any help?

Yeah, me neither. It certainly comes out the mathematics (i.e., the vorticity is zero), but it is certainly hard to track down from the Euler equations using physical reasoning. I don't know whether it is worth it spending time trying to do this.

Also, and I know this is off topic a little, but when deriving Bernoulli's equation from Navier Stokes, how do we know it is only valid along a streamline? At the very end of my derivation, assuming Newtonian, incompressible, inviscid, irrotational flow I have $\nabla(\partial_t \phi + |\vec{u}|^2/2+p/\rho + g z) = \vec{0} \implies \partial_t \phi + |\vec{u}|^2/2+p/\rho + g z = const.$ where I think the constant implies something about which streamline you're on. Also, $\vec{u}=\nabla \phi$.

Can you please submit this as a separate thread.

 

[member 428835]

Well, if the stream function satisfies Laplace's equation and the streamlines become parallel at large x, then $\partial \psi /\partial x=0$. Therefore, we are left with $\partial^2\psi /\partial y^2=0$. That automatically gives equal streamfunction spacing.

Yeah, me neither. It certainly comes out the mathematics (i.e., the vorticity is zero), but it is certainly hard to track down from the Euler equations using physical reasoning. I don't know whether it is worth it spending time trying to do this.

Thanks a ton! This makes sense.

 

[Nidum]

(1) If you look at a simplified version of this problem translated into 2D then the sloping surfaces look very similar to aircraft wings - one normal and one inverted .

There have been many studies of the air flow around wings - both for proper wings profiles and for flat plates . There have also been studies about water flow around hydrofoils though these are harder to find . For water flow and for pseudo incompressible flow of air the flow patterns are similar at lower speeds .

Using information from these sources it should be possible to sketch a reasonable 2D approximation to the flow patterns around the sloping surfaces provided that the two surfaces are well separated .

It may also be possible to sketch an approximation of the full axisymmetric flow pattern by sweeping the 2D pattern for anyone surface around the central axis .

Flow patterns can be expected to alter depending on the angle of attack of the sloping surface . Accuracy of sketched flow patterns would probably be quite good for low angles of attack and less good for high angles of attack .

(2) Studies have also been done regarding flow of air through a wind sock and flow of water through the draught tube of a submerged turbine . Interesting background reading .

(3) There is software available for drawing idealised flow streamline patterns . Drawing these patterns is much less computationally demanding than for full CFD analysis .

(4) Sketching flow patterns used to be one of the skills learned by young engine designers . Usually the flow net was sketched rather than just the streamlines .