pinkerpikachu
- 27
- 0
Homework Statement
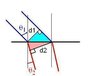
A laser beam of diameter = 3.1mm in air has an incident angle = 26 degrees at a flat air-glass surface.If the index of refraction of the glass is n=1.5, determine the diameter of the beam after it enters the glass.
Homework Equations
n1sinθ1=n2sinθ2
The Attempt at a Solution
okay, well the initial application of snell's law is obvious. The laser is going from air, where n = 1 into glass where n = 1.5
So, (1)sin(26) = (1.5)sinθ2
θ2 = (approx) 17 degrees or 16.99
I know how to find the diameter of the laser, the solutions have this equation:
d1/cosθ1 = d2/cosθ2
and simple plug and chug would yield the answer 3.3 mm
But I just don't understand where this second equation came from. Can some one walk me through the sense behind it? My book doesn't even mention it, so perhaps its obvious (just not to me).