RiotRick
- 42
- 0
Homework Statement
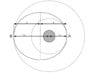
Consider an elliptical orbit of a satellite (of mass m)
around the Earth (of mass M >> m). The perigee is at ##r_A## and the apogee at ##r_B##, as measured
from the centre of the Earth, itself located at one of the focal points of the ellipse (see Fig. 1).
We work in an Earth-centered inertial reference frame.
When at apogee, the satellite is given a kick to increase its speed, for instance by burning
fuel and ejecting propellant. Assuming that the kick is instantaneous, by how much should
its speed increase so that the satellite achieves a circular orbit at ##r_B##? Does that ##\Delta v## depend
on the satellite’s mass? Qualitatively (without making any precise calculations), does the
amount of fuel burned to achieve the ##\Delta v## depend on the mass? Justify your answer
Homework Equations
delta v from Hohmann transfer orbits
The Attempt at a Solution
I'm a bit confused about the mass.
In the formula is no mass given, so it doesn't depend on "m" but I can't justify the answer. It doesn't make sense to me. If I change the orbit, I'll change the angular momentum. The conservation of angular momentum no longer holds. That means I have to apply torque. Torque is defined as ##r \times F## but F depends on "m". My technical intuition also tells me it should depend on "m".