How Ebeb's Diagram Reveals Time Dilation

[PeterDonis]

The proper time displayed by clock B, (that is the coordinate time in frame B?), transformed by LTE gives the measurement relative to the observer A.

No. You don't transform proper time; it's an invariant, the same in all frames. Proper time is just the length along a specific curve (in this case, B's worldline) between two chosen points (whichever events on B's worldline you want to know B's elapsed time between).

IMO you should forget about coordinates altogether until you understand the underlying geometry that the coordinates are representing, which consists of the invariant lengths along particular curves, and the angles between the curves when they intersect. The "angle between the curves" in SR corresponds to relative velocity.

 

[Dale]

The proper time displayed by clock B, (that is the coordinate time in frame B?).

What have I told you before about this? In my notation above, what is the difference between $\tau_b$ and $t_B$? Where is each defined?

 

[Grimble]

The proper time displayed by clock B, (that is the coordinate time in frame B?), transformed by LTE gives the measurement relative to the observer A.

Let me rewrite what I meant here...
The coordinate time in frame B, which is synchronised to the proper time of frame B's clock (is that the right way to say it?), transformed by LTE gives the measurement relative to the observer A.[/QUOTE]

 

[Grimble]

What have I told you before about this? In my notation above, what is the difference between τ_b and t_B? Where is each defined?

τ_b is the proper time on the worldline of clock B.
t_B is the coordinate time at an event in clock B

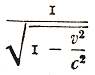
In the special case of an inertial observer in special relativity, by convention the coordinate time at an event is the same as the proper time measured by a clock that is at the same location as the event, that is stationary relative to the observer and that has been synchronised to the observer's clock using the Einstein synchronisation convention.

So, I read this as meaning that τ_ba1 is equal to t_Ba1 is that right?

 

[Dale]

τ_b is the proper time on the worldline of clock B.
t_B is the coordinate time at an event in clock B

Yes.

So, I read this as meaning that τ_ba1 is equal to t_Ba1 is that right?

No. If I understand what you are trying to denote here then $\tau_{ba1}$ doesn't exist. That would be the proper time of clock b at event a1. But event a1 is not on the worldline of clock b. So it is undefined.

 

[Grimble]

I have tried to take in all I have been told and apply it to the scenario of moving clocks.
I now understand that proper time involves measurement along a single dimension between events that occur on a clock's worldline.
In Fig. A I have drawn two clocks, A & B.
Event τ_a0.0 and Event τ_b0.0 are a single event that occurs when the two clocks are co-located. The clocks then move apart. The lights emitted at the common event labelled a0.0/b0.0 strike their respective mirrors after 1 second, having each traveled 1 light second.

​

 

[Dale]

@Grimble I have looked fairly carefully at your diagram and although it is pretty complicated, I think I understand it. Most of them seem correct to me, but Fig A and Fig 5 have some problems. You have labeled several spatial locations with $\tau_a$ or $\tau_b$ but in this case the proper time should only label the worldline of the end of the clock. So all of the $\tau$ labels should be on the horizontal axis.

 

[Grimble]

@Grimble I have looked fairly carefully at your diagram and although it is pretty complicated, I think I understand it. Most of them seem correct to me, but Fig A and Fig 5 have some problems. You have labeled several spatial locations with $\tau_a$ or $\tau_b$ but in this case the proper time should only label the worldline of the end of the clock. So all of the $\tau$ labels should be on the horizontal axis.

Thank you Dale, I can see that, I am finding it difficult to draw what I was trying to shew. Would it be better to label Fig. A as the diagram of the lights within the clocks, as it is the lights that travel to the mirrors whereas the clocks are stationary (within their individual frames)?

How should one draw a diagram shewing proper time?

 

[Dale]

Would it be better to label Fig. A as the diagram of the lights within the clocks, as it is the lights that travel to the mirrors whereas the clocks are stationary (within their individual frames)?

There is no proper time along the worldline of a pulse of light. Proper time is defined along timelike worldlines only.

 

[Grimble]

There is no proper time along the worldline of a pulse of light. Proper time is defined along timelike worldlines only.

Thank you, I wondered if that would be the case...
I think using a light clock is causing complications, and is unnecessary for what I am trying to do. I suppose it was a way to help me visualize time by the movement of the light. I can now see how it does that but at the same time how it muddies the waters.
So I have changed my diagram to represent two clocks and their proper times plotted on their worldlines.

The purpose of this diagram is to highlight that proper time is the same for every perfect clock that ticks at the same rate of 1 second per second. Which brings me to another realisation: coordinate time is individual to each reference frame, being relative to that frame. Proper time is invariant because it is only measured relative to its own frame, in this case to the frame of each clock.
Proper time is the measurement of time by a clock and in that clock's frame the clock is at rest and its worldline moves in one dimension, that of time. A worldline only moves through space when viewed by an observer outside the clock's frame.

So I hope I am right if I say that clock A and clock B will each record (and display) time at the same rate, that in Spacetime an observer can read the invariant proper time from either clock, but will measure the clock to run slow as a function of its relative motion?

 

[Dale]

I have changed my diagram to represent two clocks and their proper times plotted on their worldlines.

That is better, but I am not sure what the vertical axis represents now. Previously it was a second direction in space. If it were now representing time then you would need to show them as non-parallel since they are moving away from each other.

 

[Grimble]

If proper time is seen as one dimensional, how does that work? For it seems to me that the 1D must be time, but if that is the case then how can two 1D paths, for the two clocks be non-parallel for being 1D direction would have no meaning?
Anyway I have redrawn it as two separate diagrams Fig. A and Fig. B; what I am trying to convey is the idea that proper time works in exactly the same way for any clock, or other object.
In its own reference frame an object is at rest and only moves through time?
And time progresses at the same rate everywhere in every frame - c.
It seems to me there is a dichotomy between proper time, which, is invariant because it is measured directly along an objects worldline and coordinate time which is measured remotely from a particular observer's perspective and is therefore specific to each observer.

 

[Ibix]

A piece of spaghetti is one dimensional - or close enough for this example - but if you lay a dozen pieces out parallel they form the lines of a grid.

Coordinate time is just what happens when you agree on a direction to call "time" and a procedure for defining "time zero".

 

[Grimble]

But when you add more pieces of spaghetti and form a grid are you not adding more constraints that are nothing to do with our one dimensional proper time? Even when two worldlines interact are they not still separate 1 dimensional lines?

 

[Ibix]

But when you add more pieces of spaghetti and form a grid are you not adding more constraints that are nothing to do with our one dimensional proper time?

Yes. That's what a simultaneity convention is - an arbitrary choice out of many possible ways to define "the same time not at the same place".

 

[sweet springs]

Hi.

I would like to return to the question of how this diagram, courtesy of 'Ebeb' from #124 in thread "Proper (and coordinate)

In A system, velocities of A,O,B are
A: 0
O: V
B: about 2V, exactly $\frac{2V}{1+\frac{V^2}{c^2}}$

In O system, velocities of A,O,B are
A: -V
O: 0
B: V

In B system, velocities of A,O,B are
A: about -2V, exactly $-\frac{2V}{1+\frac{V^2}{c^2}}$
O: -V
B: 0

The three systems have their proper times and time of other systems are slow according to their velocities. Diagram of O is as you showed. In diagram of A, Lines of O and B lie right side. In diagram B, Lines of A and B lie left side. A and B seem to have same proper time only for O not for other systems.
Best.

 

[Dale]

Anyway I have redrawn it as two separate diagrams Fig. A and Fig. B; what I am trying to convey is the idea that proper time works in exactly the same way for any clock, or other object.

Ok, as two separate figures that makes sense.

It seems to me there is a dichotomy between proper time ... and coordinate time

Most definitely, yes. That is why I was being such a stickler about using them correctly. They are fundamentally different things.

 

[sweet springs]

PS to #51

the proper time = τ, the distance to the mirror is cτ
the coordinate time = t the distance to B's mirror is ct
the distance between A and B is vt
and (cτ)2 = (ct)2 - (vt)2
Yes the proper time squared (which is another way of saying the Spacetime interval) is equal to the coordinate time squared minus the distance squared.

World interval between A clock ticks 0:00 and A clock ticks 1:00 is $ct_A$. This is minimum time of all the systems because $$t_A < t =\frac{\sqrt{c^2t_A^2+x^2}}{c}$$
World interval between O clock ticks 0:00 and O clock ticks 1:00 is $ct_O$. This is minimum time of all the systems because $t_O < t =\frac{\sqrt{ct^2_O+x^2}}{c}$
World interval between B clock ticks 0:00 and B clock ticks 1:00 is $ct_B$. This is minimum time of all the systems because $t_B < t =\frac{\sqrt{ct^2_B+x^2}}{c}$

So the system in which two events occur at the same place has minimum time interval among all the systems. In your mirror setting, light path is clock at rest 0:00, mirror 0:30 and clock at rest again 1:00. Proper time of things in motion is known and shared with all the systems calculating $\frac{\sqrt{c^2t^2-x^2}}{c}$ respectively. Best.

 

[jbriggs444]

But when you add more pieces of spaghetti and form a grid are you not adding more constraints that are nothing to do with our one dimensional proper time? Even when two worldlines interact are they not still separate 1 dimensional lines?

Let's be clear. @Ibix called for strands of spaghetti laid out parallel. He did not call for any cross-wise strands. As I understand the analogy:

The strands are clocks. One end is when they are started. The other end is when they are stopped.

You can lay out strands in parallel (a bunch of clocks at rest with respect to one another). You can line up their ends (you can start them all "at the same time" in some fashion). You can do this with the start times at right angles to the strands. Or you can do it on a slant.

But if the start points are "all at the same time" and are not all at the same place, you are not allowed to have a strand of spaghetti that goes through all of them. They are space-like separated. A clock cannot go from anyone to any other. A cross-wise line of synchronization is not a strand of spaghetti.

 

[sweet springs]

Hi. For whom spaghetti is vertical in his tx diagram, it is time spaghetti, e.g. 8:00 car and 9:00 car. However for whom same spaghetti is perpendicular it is time-space mixed spaghetti. It has both time interval length and space interval length, e.g. 8:00 home and 9:01 office.

Time spaghetti for A is time-space spaghetti for B and vice versa. Length of spaghetti is defined as time interval of A for whom spaghetti is time-one not time-space one.

 

[Ibix]

However for whom same spaghetti is perpendicular it is time-space mixed spaghetti.

You can't have perpendicular timelike vectors. You can certainly have non-parallel ones, but never perpendicular. For any time-like vector there exists a frame in which it is parallel to (1,0,0,0). The inner product of any time-like vector with this is clearly non-zero.

 

[sweet springs]

Thanks. Oblique, not perpendicular, due to my poor English. Best.

 

[Grimble]

Now it seems you are trying to befuddle me with spaghetti!
I have just come to accept that 1D spaghetti is a unique representation of each clock; and that as soon as one refers to multiple strands, whether parallel, orthogonal, oblique, or tied in knots, you have to be referring to coordinate times, not proper time.

I can understand that when one reduces spacetime diagrams to 2 or 3 dimensions, time is drawn vertically for a frame, so a resting object does not move as time increases. And to extend that to 4 dimensions one could leave space to the 3 cartesian coordinates, but then time would have to be somehow drawn so that while extending it did not move in any physical direction.

So in my amateurish way of thinking I imagine drawing time as a spherical coordinate; it would be like measuring the time like a flash of light - moving at c in every direction...
And that drawing it vertically would then be merely a convention.
For how can one assign a direction to proper time? To assign it a direction one must add extra dimensions.

This one way I visualize the difference between proper and coordinate times; for proper time, Fig 58A there is only one dimension and it has no direction; for coordinate time we add coordinates for the spatial dimensions: we know that when Clock B has traveled 0.6 light seconds along the x axis, the light in clock B will have traveled 1 light second from the null point. Therefore the point where the light is after 1 second measured by the observer is fixed by the movement of the clock. It has, therefore a full set of coordinates. It is coordinate time.

(Please note I did not intend these diagrams to conform to any specific diagram 'type', but merely to shew how I visualize it.

 

[sweet springs]

I have just come to accept that 1D spaghetti is a unique representation of each clock; and that as soon as one refers to multiple strands, whether parallel, orthogonal, oblique, or tied in knots, you have to be referring to coordinate times, not proper time

More appropriate name for spaghetti is world-line, straight lines as drawn in your figure in OP. World line is space-time like but if events to be considered are given we can choose special coordinate that world line through the events is time-like. Events on this world-line has common place to occur in that coordinate. The coordinate time of this special coordinate is called proper time. Propertime is one of coordinate times.

 

[jbriggs444]

World line is space-time like but we can choose special coordinate that world line is time-like.

A time-like world line is always time-like regardless of coordinates. There is no such thing as a "space-time like" world line.

What is true is that in a coordinate system where a clock is at rest, one second of coordinate time is traversed for every second of proper time that the clock ticks off.

 

[sweet springs]

Thanks. Again my misuse of words, I am afraid. How about Only time component and No space component, instead of "time-like" and Both time and space components, instead of "time-space like" in my previous post ? All lines here expressing motion of body are time-like as you taught. Best.

 

[jbriggs444]

Thanks. Again my misuse of words, I am afraid. How about No space component, instead of "time-like" and Both time and space components, instead of "time-space like" in my previous post ? Best.

The correct terms are "time-like", "space-like" and "null". Those are invariant properties of an interval. That is to say that they do not depend on choice of coordinate system.

The terms "time-space like" and "space-time like" are never used. Those would not refer to invariant properties.

 

[sweet springs]

Hi.

So in my amateurish way of thinking I imagine drawing time as a spherical coordinate; it would be like measuring the time like a flash of light - moving at c in every direction...

Your chart seems like 2d radar charts as in the back of video . I have no idea of your "spherical time coordinate".

 

[jbriggs444]

Now it seems you are trying to befuddle me with spaghetti!
I have just come to accept that 1D spaghetti is a unique representation of each clock; and that as soon as one refers to multiple strands, whether parallel, orthogonal, oblique, or tied in knots, you have to be referring to coordinate times, not proper time.

@Ibix proposed parallel strands. That translates to a set of unaccellerated clocks all at rest with respect to one another.

Straight strands = unaccelerated.
Parallel = at rest with respect to one another.

Let's not think about knots until we have parallel strands sorted.

The distance along any particular strand of spaghetti is analogous to proper time.
If you lay the spaghetti on a sheet of graph paper, the grid lines in the horizontal direction mark out coordinate time.

Note that the analogy is imperfect because spaghetti can be rotated past 45 degrees on a sheet of Euclidean graph paper. Clocks cannot do a rotation past 45 degrees on a space-time diagram.

 

[Dale]

So in my amateurish way of thinking I imagine drawing time as a spherical coordinate

Please, don't do that. You really need to stop just making things up on your own. Please just try to learn and use the standard techniques.

For how can one assign a direction to proper time?

Proper time is not a direction. It is the spacetime equivalent of length.

If you have two points on a piece of paper and you connect them with a line then you can measure the length along that line from the first point to the second. Similarly, if you have two events in spacetime and you connect them with a worldline then you can measure the proper time along that worldline from the first event to the second.

This one way I visualize the difference between proper and coordinate times; ...

The difference between proper time and coordinate time is the difference between coordinates and lengths. Please stop making stuff up

 

[Grimble]

I am sorry if you think that, but I am not trying to make things up but to explore what they mean.
I now understand that propertime is one dimensional; which means it is the time measured between events on a worldline. (It would be wrong to describe it as the propertime measured on a worldline because we are defining propertime).
Propertime in invariant. It is the same whoever is measuring it. That can only be because it is measured between points on a worldline, in that dimension alone. It can have no location, nor direction. For the 'clock' whose time is being measured it happens at a single location - that of the clock; For a different observer it may be between different physical locations, but only the duration of the interval measured on the clock is relevant.

So, if we liken the single dimension of proper time to spaghetti, the length of the spaghetti is the proper time, its direction, whether it is straight, parallel or twisted in knots is meaningless.

 

[Ibix]

I now understand that propertime is one dimensional; which means it is the time measured between events on a worldline. (It would be wrong to describe it as the propertime measured on a worldline because we are defining propertime).

It's the time measured between two events along a worldline that passes through those events. Thus two observers may experience two different times between a pair of events if they follow different worldlines. That's the resolution of the twin paradox, in one line.

That can only be because it is measured between points on a worldline, in that dimension alone.

Careful with "dimension" here. Better to say that the proper time for a worldline is defined only on that worldline and leave "dimension" out of it.

It can have no location, nor direction

Depends a bit what you mean. I'd agree that direction in spacetime isn't related to proper time. However there is a clear meaning to "along the worldline in the direction of increasing proper time".

So, if we liken the single dimension of proper time to spaghetti, the length of the spaghetti is the proper time, its direction, whether it is straight, parallel or twisted in knots is meaningless.

Well, it's not meaningless. It's irrelevant to the proper time, though, which is what I suspect you meant.

Note that proper time is only defined for time-like worldlines and these cannot curve back on themselves in flat spacetime. So no knots. The rest is fine.

 

[jbriggs444]

Propertime in invariant. It is the same whoever is measuring it

This piece needs some additional details. Indeed, proper time is invariant. It is the same regardless of what reference frame is used to measure it. But "measure" means that there has to be some physical procedure to come up with the measurement. How does a fellow using reference frame B "measure" the proper time between when clock a at rest in frame A starts and stops ticking?

A fellow at rest in frame B could measure it by using a telescope and copying down the readings of clock a when it starts and stops. He could subtract one from the other and say "there -- that's my measurement of proper time". That would be a valid measurement procedure. It is obvious that such a measurement procedure would produce an invariant result. No matter what frame of reference is used, the difference between the readings of clock a when it starts and stops will be the same. This measurement procedure is uninteresting. Let us not use it. Instead...

Let the fellow using frame B lay out rulers at rest in his frame to establish a three dimensional coordinate grid. He could then use clocks at rest in his frame and synchronized in his frame to extend this to a four dimensional coordinate grid. He could then note the coordinate position and time (x_i, y_i, z_i, t_i) at which clock a starts ticking. He could note the coordinate position and time (x_f, y_f, z_f, t_f) at which clock a stops ticking.

The fellow in frame B could then calculate $\sqrt{(t_f-t_i)^2 - (x_f-x_i)^2 - (y_f-y_i)^2 - (z_f-z_i)^2}$ (all using coordinates from frame B).

Now we have an interesting question: Is this number equal to the difference between the starting and stopping times read directly from the face of clock a?

The claim is that yes, this calculated figure will be the same regardless of what frame of reference is used to do the measurement and will match the difference between the starting and stopping times read directly from the face of clock a.

For example, the fellow in frame B could measure a five second elapsed time and a three light-second displacement for clock a. He would then calculate a four second proper time.

 

[sweet springs]

Hi. World interval between the events is invariant. Everybody in any coordinate can observe it using clocks and measures and gets the same value. Among them one observer is privileged to observe world interval only by clock without measure. The events happen at the same place for him so he does not have to measure space between the events. Zero. In respect to him invariant world interval is called proper time. Proper time is time or coordinate time for him but square root of time^2 - space^2 for all the others.

Analogy in 2d geometry. Unit circle in xy plane
$x=cos\theta$
$y=sin\theta$
By rotation we can live in the coordinate where X=1,Y=0.
In respect to this simplicity let us call the radius of circle Proper x.
$Proper \ x = \sqrt{X^2} =\sqrt{x^2+y^2}=1$
Best.

 

[Ibix]

Among them one observer is privileged to observe world interval only by clock without measure.

...assuming the events are time-like separated. If they're null- or space-like separated there is no observer who can do this.