ClearWhey
- 19
- 4
- Homework Statement
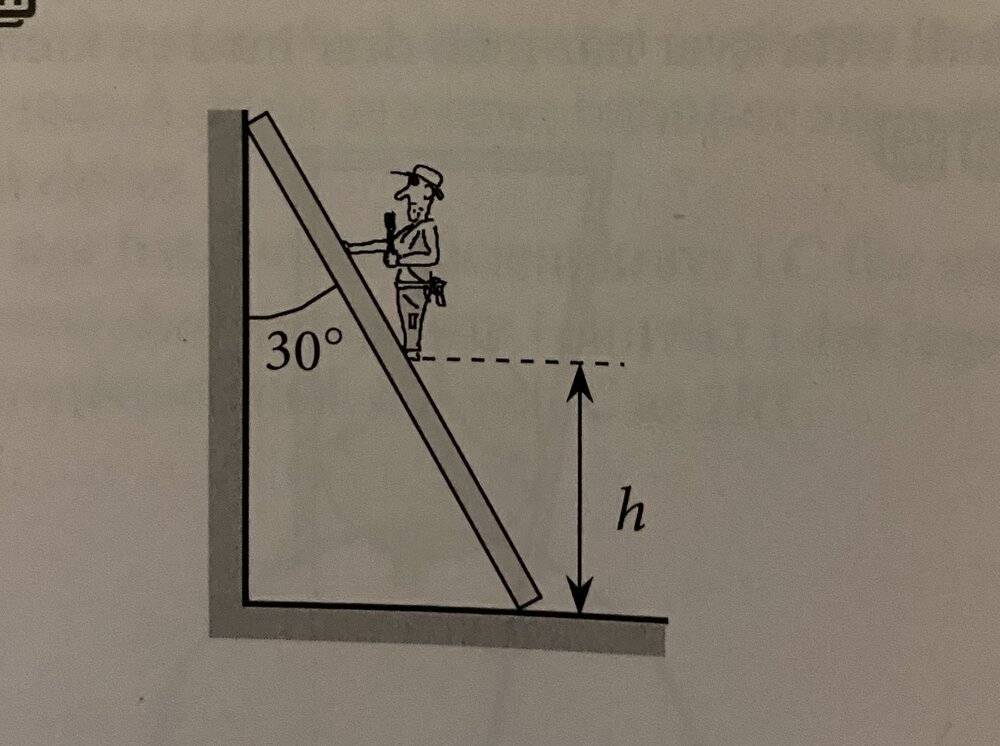
- A person climbs a ladder like in the picture, how far can he climb up before the ladder starts sliding?
- Relevant Equations
- Ladder length 4m
Person weight 60kg
Ladder weight 10kg
Ladders coeficient of friction on both contact points 0,35
Look on picture two for my equations, I’m pretty sure my first three equations are correct as it’s the same on the answer paper I got. Answer paper only shows the three equations and correct answer so I have no idea how they got to it.
When I put the equations togheter And solve out ”h” i get like 1,5m something which is wrong. The answer is 2,34m. Can someone please look into this, did I simplify the equations wrong? Or is it something else. Have tried myself for like 2-3 hours and this is my last resort. Thanks in advance!
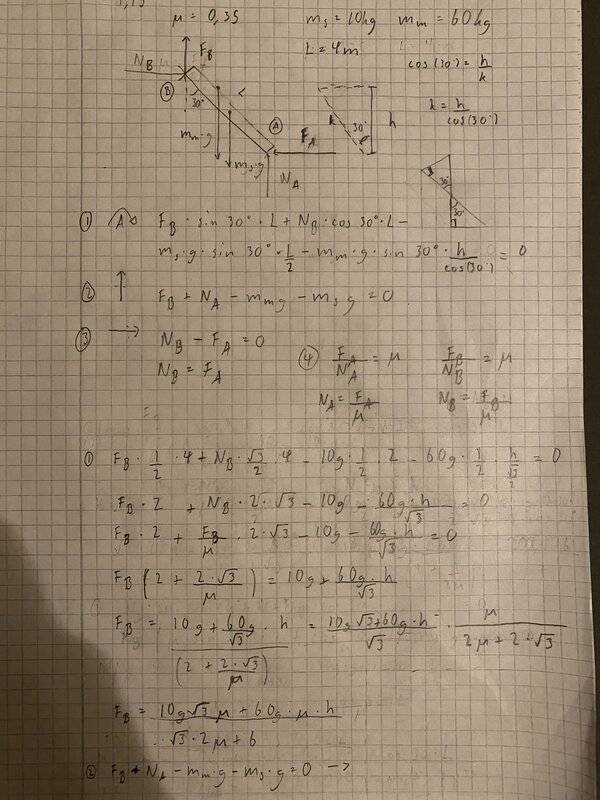
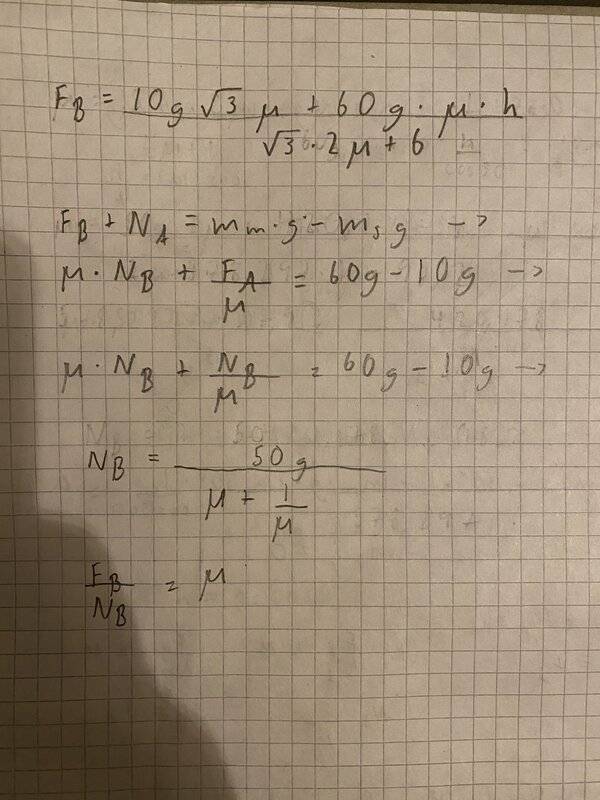
When I put the equations togheter And solve out ”h” i get like 1,5m something which is wrong. The answer is 2,34m. Can someone please look into this, did I simplify the equations wrong? Or is it something else. Have tried myself for like 2-3 hours and this is my last resort. Thanks in advance!