tom23
- 4
- 0
Another Physics question??
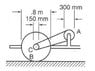
The cart shown below is pulled at a speed of 5 km/hr to the right. Determine the speed of the belt, and the rotational speed of roller A.
Please see figure attached
I got the speed of the belt as 0.26 m/s and rotational speed as 1.7375 rad/s. I was wondering if I got the right answer.
Homework Statement
The cart shown below is pulled at a speed of 5 km/hr to the right. Determine the speed of the belt, and the rotational speed of roller A.
Please see figure attached
Homework Equations
The Attempt at a Solution
I got the speed of the belt as 0.26 m/s and rotational speed as 1.7375 rad/s. I was wondering if I got the right answer.