henrco
- 46
- 2
Hi,
Could i please get advice on this problem and confirm that my approach and solution are correct?
Thanks in advance.
1. Homework Statement
An enemy space rocket traveling at speed 0.8c towards the planet Zog fires a missile in the direction parallel to its own path. Relative to the rocket, the missile travels at v = 0.6c.
a)How long will the missile take to reach Zog if it is 2 light years distant (in the rest frame of the planet) at the
time of firing?
b) Find the relative speed of the missile to the rocket:
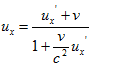
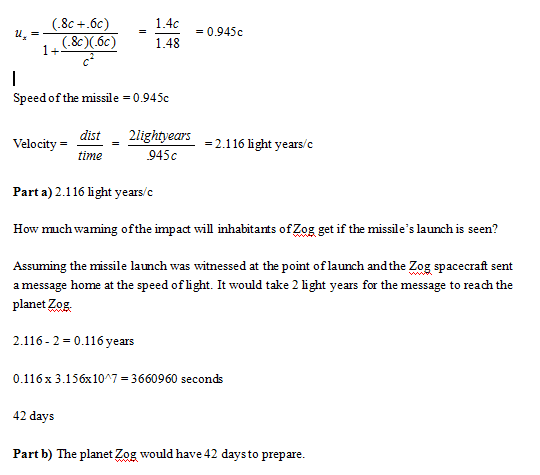 [/B]
[/B]
Could i please get advice on this problem and confirm that my approach and solution are correct?
Thanks in advance.
1. Homework Statement
An enemy space rocket traveling at speed 0.8c towards the planet Zog fires a missile in the direction parallel to its own path. Relative to the rocket, the missile travels at v = 0.6c.
a)How long will the missile take to reach Zog if it is 2 light years distant (in the rest frame of the planet) at the
time of firing?
b) Find the relative speed of the missile to the rocket: