How Is Electric Force Balancing a Suspended Charged Ball in a Capacitor?

[stuplato]

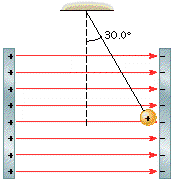
A small plastic ball of mass 6.10 10-3 kg and charge +0.150 µC is suspended from an insulating thread and hangs between the plates of a capacitor (see the drawing). The ball is in equilibrium, with the thread making an angle of 30.0° with respect to the vertical. The area of each plate is 0.0150 m2. What is the magnitude of the charge on each plate?
.

.
I tried several times and the most reasonable answer I get is .9715 m but wrong... Thanks in advance

 

[Astronuc]

Please show your work.

This is a statics problem. The electric force = F_e = qE must equal the restoring force for a net force of zero on the ball.

Start by determing the restoring force on the ball, i.e. the gravitational force. Write out the force balance equation.