jisbon
- 475
- 30
- Homework Statement
- The energy band in a semiconductor sample is given by
##6.67x^2##
eV, where x is the distance and is valid from 0 to 3m.
(i)Sketch energy band diagram, indicating valence and conduction bands, energy gap and direction of x.
(ii)Determine the electric field in terms of V and m as a function of distance x and indicate the direction of the electric field in the energy band diagram.
(iii)Calculate the electric field at x=3m (in terms of and m)
- Relevant Equations
- -
This is my attempt at this question, and I'm probably wrong, will need some help/guidance from the experts here :/
i)
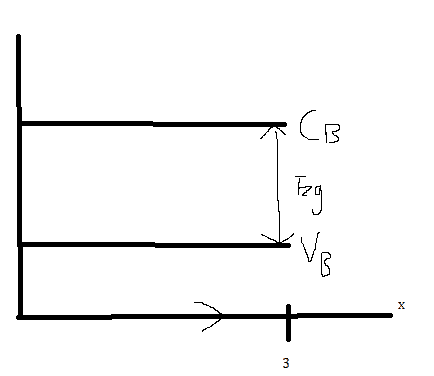
(ii)
Since energy band given by ##6.67x^2##, can I assume that electric field is simply the energy difference from 0-3m divided by 3m? In this case, would the answer simply be (6.67*3*3)-(6.67*0*0)/3= 20.01V/m?
(iii)At x=3, will the electric field be simply 20.01*3=60.03?
Cheers
i)
(ii)
Since energy band given by ##6.67x^2##, can I assume that electric field is simply the energy difference from 0-3m divided by 3m? In this case, would the answer simply be (6.67*3*3)-(6.67*0*0)/3= 20.01V/m?
(iii)At x=3, will the electric field be simply 20.01*3=60.03?
Cheers