How Much Work Does Gravity Do on an Ice Flake in a Bowl?

[stargirl17]

Homework Statement

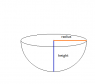
a 2.00 g ice flake is released from the edge of a hemispherical bowl whose radius is 22.0 cm. the Flake-bowl contact is frictionless. How much work is done on the flake by the gravitational force during the flake's descent to the bottom of the bowl?

Homework Equations

w=fd

The Attempt at a Solution

do i use 9.81 m/s^2 as the force?
and how do i know the distance?

 

[Kabbotta]

If you were sitting on the edge of a cereal bowl and you slid down to the bottom of the bowl how far vertically would you have fallen? You've been given that.

9.8 m/s^2 is the acceleration of gravity. You need a force, mass * acceleration.

Then you've got the only equation you needed.

 

[rock.freak667]

What is the distance between the bottom of the hemisphere and the top of the hemisphere?

 

[Kabbotta]

Hopefully this helps, it's not too complicated so don't over think it.

 

[rock.freak667]

Hopefully this helps, it's not too complicated so don't over think it.

I was asking you. The hemisphere is half of a sphere, so the center to any point on the surface is a radius, so what is the height of the sphere?

(By height, I mean the vertical distance the ice flake travels to the bottom of the sphere)

 

[Kabbotta]

The snowflake starts at the edge of a hemispherical bowl so the height is equal to the radius.

In your case,
W = mgr

If there was a full sphere, the height from top to bottom would be the diameter or 2*radius.

 

[Kabbotta]

What is the distance between the bottom of the hemisphere and the top of the hemisphere?

This height is equal to the radius of the hemispherical bowl that is directly given in the question. So in this case,

W = mgr

 

[rock.freak667]

This height is equal to the radius of the hemispherical bowl that is directly given in the question. So in this case,

W = mgr

I apologize, I did not see your post before mine. But I was not asking for my clarity, I was asking the OP.

 

[Kabbotta]

Oh, I see, your post makes a lot more sense now ; )
No problem.